1. Condensateur

Définition – Rôle et représentation symbolique

Un condensateur est formé de deux conducteurs métalliques appelés armatures séparés par un matériau isolant (diélectrique). Son rôle est d'emmagasinée de l'énergie électrique lors de sa charge et de la restituée lors de sa décharge,

Le condensateur est représenté symboliquement par : 

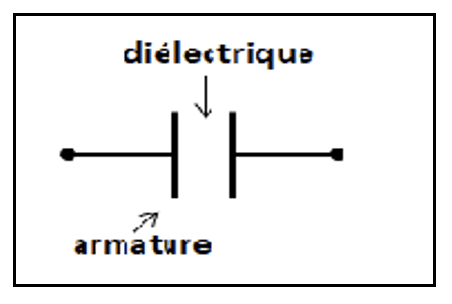
capture-decran-2025-02-21-a-073708

Convention récepteur pour un condensateur

L'une des armatures est chargée positivement et l'autre négativement.
Un condensateur en convention récepteur est représenté : 

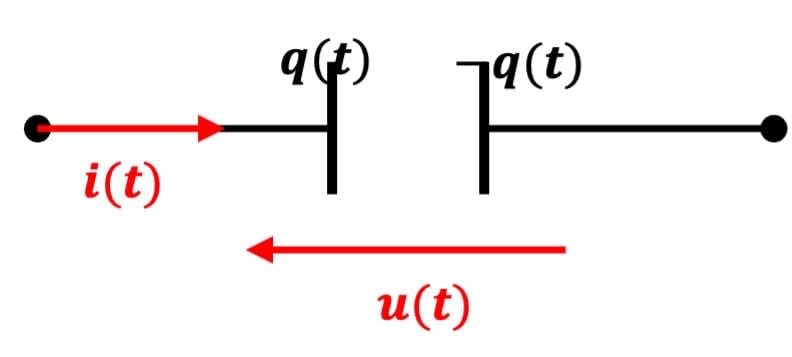
tle-s2pccondensateurmc2

2. Caractéristiques d'un condensateur

Capacité d'un condensateur

L'expérience montre que la charge $q$
d'un condensateur et la tension $U$ entre ses bornes sont liées par la relation :
$$q = CU$$

Le coefficient de proportionnalité $C$ est appelée capacité du condensateur.

Unités : $q$ en coulomb (C) ; $U$ en volt (V) et $C$ en farad (F).

3. Relation entre la charge électrique et l'intensité du courant

En convention récepteur, l'intensité $i$ du courant à un instant quelconque de date $t$ est égale à la dérivée de la
charge $q$ par rapport à $t$. $i=\dfrac{dq}{dt}$

Soit A et B les deux armatures du condensateur, $q_a$ la charge de l'armature A, $q_B = -q_a$ la charge de l'armature B. 

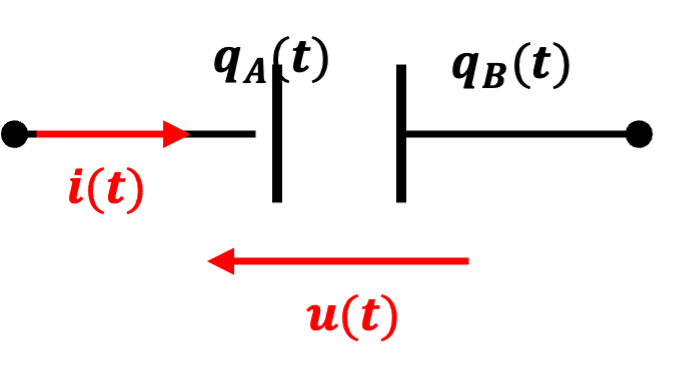
tle-s2pccondensateurmc3

Le sens de parcours du courant étant défini, on aura donc :
$i = \dfrac{dq_A}{dt} = -\dfrac{dq_B}{dt}$

Conséquence : Relation intensité-tension
En remplaçant l'expression : $q = CU_{AB}$ dans la relation précédente, il vient :
$i = \dfrac{du_{AB}}{dt} = \dfrac{d(CU_{AB})}{dt} = C\dfrac{U_{AB}}{dt}$

4. Association de condensateurs

En série :
$\dfrac{1}{C_{eq}} = \dfrac{1}{C_1} + \dfrac{1}{C_2} \Rightarrow$ généralisation : $\dfrac{1}{C_{eq}} = \displaystyle\sum \dfrac{1}{C_i}$

En parallèle : $C_{eq} = C_1 + C_2 \Rightarrow$ généralisation : $C_{eq} = \displaystyle \sum C_i$

5. Charge et décharge d'un condensateur

Dispositif expérimental 

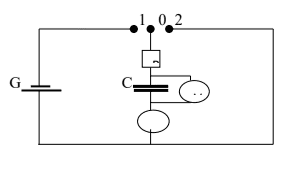
G : générateur
g : galvanomètre
R : résistor
C : condensateur
V : voltmètre
K : interrupteur

Charge d'un condensateur

Plaçons l'interrupteur K en position 1 :


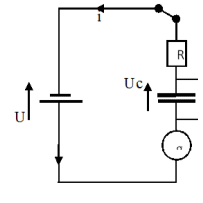
Équation différentielle vérifiée par $U_c$
$E = U_c + RC\dfrac{dU_c}{dt}$ avec $\tau = RC$
La solution de l'équation différentielle est :
$$U_c = E(1- e^{\dfrac{-t}{RC}})$$
Équation différentielle vérifiée par $q$ :
$CE = q + RC\dfrac{dq}{dt}$
La solution de l'équation différentielle est :
$$q = CE(1-e^{\frac{-t}{RC}})$$
Intensité du courant de charge :
$i=\dfrac{E-t}{R} = \dfrac{E}{R}e^{\frac{-t}{RC}}$

Constante de temps RC du dipôle RC :
La durée $t = R.C$ est caractéristique de l'évolution du système. Elle donne un ordre de grandeur du temps que met la tension $U_c$ pour atteindre la valeur $E$ : C'est la durée au bout de laquelle la tension du condensateur atteint 63% de sa valeur maximale.

  • Détermination expérimentale de $t$
    • Méthode de la tangente à l'origine
    • Méthode des 63% : $\tau$ temps correspondant à $U_c = 0.63 E$ 

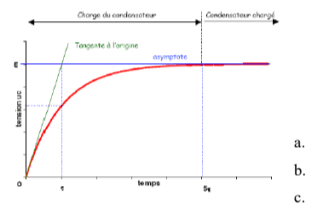
Charge d'un condensateur

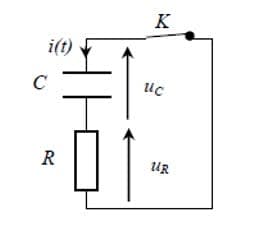
tle-s2pccondensateurmc4

  • Équation différentielle par $U_C$ lors de la décharge du condensateur : 
    $RC\dfrac{du_c}{dt} + U_c = 0$
    Solution de l'équation différentielle :
  • Équation différentielle vérifiée par $q$ lors de la décharge :
    $R C \dfrac{d q}{d t}+q=0$
    Solution de l'équation différentielle :
    $q = CU = CEe^{\frac{-t}{RC}}$
    Intensité du courant de la charge :
    $i=\dfrac{-E}{R}e^{\frac{-t}{RC}}$


La durée $t = R.C$ est caractéristique de l'évolution du système. Elle donne un ordre de grandeur du temps que met la tension $U_c = E$ pour atteindre la valeur 0 : c'est la constante de temps.

  • Détermination expérimentale de $t$
    • Méthode de la tangente à l'origine
    • Méthode des 37% : $\tau$ temps correspondant à $U_c = 0.37 E$ 

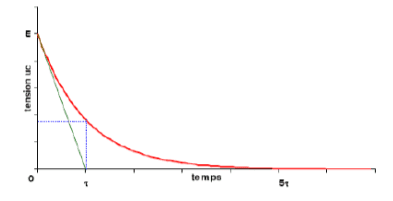
Energie emmagasinée dans un condensateur : $W = \dfrac{q^2}{2C} = \dfrac{CE^2}{2}$