1. Transformation rapide – Transformation lente

  • Une transformation est considérée comme rapide lorsque sa durée est trop courte pour que l'on puisse apprécier la vitesse ; elle paraît se faire dès que les réactifs sont en contact.
  • Une transformation est lente si elle dure quelques secondes, voire des heures, des jours, des mois ou des années (réactions très lentes).

2. Vitesses de réaction

Vitesse de formation

Elle concerne un produit de la réaction.

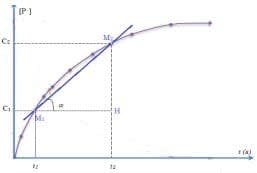
  • Vitesse moyenne de formation : soient $n_1$ le nombre de moles formées de produit à la date $t_1$ et $n_2$ la quantité de matière de produit formé à la date $t_2$. La vitesse moyenne de formation du produit est : 

$\displaystyle v_{\rm{moy}} = \dfrac{n_2 - n_1}{t_2 - t_1} = \dfrac{\Delta n}{\Delta t}$ s'exprime en $\rm mol.s^{-1}$ ou usuellement en $\rm mol.min^{-1}$ ou $\rm mol.h^{-1}$.

Pour un volume $\rm V$ constant on peut utiliser la variation des concentrations : 

$\displaystyle v_{\rm{moy}} = \dfrac{C_2 - C_1}{t_2 - t_1} = \dfrac{\Delta C}{\Delta t}$

Graphiquement, $V_m$ correspond à la pente de la droite passant par les deux points $\rm M_1(t_1,C_1)$ et $\rm M_2(t_2,C_2)$.

capture-decran-2025-02-28-145814

  • Vitesse instantanée de formation : c'est une vitesse moyenne calculée sur une durée très petite ($\Delta t$ tend vers zéro).

Cela donne la dérivée par rapport au temps du nombre de moles $n$ ou de la concentration : 

$\displaystyle v(t) = \dfrac{dn_p}{dt}$ ou $\displaystyle v(t) = \dfrac{dC}{dt}$

Graphiquement, $V$ correspond à la pente de la tangente à la courbe $n=f(t)$ au point $\rm C$ d'abscisse $t_0$ considérée.

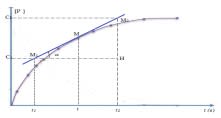
capture-decran-2025-02-28-145932

$\displaystyle v_{\rm{moy}} = \tan \alpha = \dfrac{M_2H}{M_1H} = \dfrac{C_2 - C_1}{t_2 - t_1} = \dfrac{dC}{dt}\bigg]_t$

Vitesse de disparition

Elle concerne un réactif.

  • Vitesse moyenne de disparition : Soient $n_1$ le nombre de moles du réactif à la date $t_1$ et $n_2$ celui qui correspond à la date $t_2$. La vitesse moyenne de disparition est : 

$\displaystyle v_{\rm{moy}} = \dfrac{n_2 - n_1}{t_2 - t_1} = \dfrac{\Delta n}{\Delta t}$ en $\rm mol.s^{-1}$, $\rm mol.min^{-1}$ ou $\rm mol.h^{-1}$.

Pour un volume $V$ constant on peut utiliser la variation des concentrations.

$\displaystyle v_{\rm{moy}} = \dfrac{C_2 - C_1}{t_2 - t_1} = \dfrac{\Delta C}{\Delta t}$

Cela correspond à la pente de la droite passant par les points $\rm M_1(t_1,C_1)$ et $\rm M_2(t_2,C_2)$.

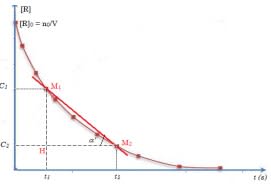
capture-decran-2025-02-28-150237

$\displaystyle v_{\rm{moy}} = \tan \alpha' = \dfrac{M_1H}{M_2H} = \dfrac{C_2 - C_1}{t_2 - t_1}$

  • Vitesse instantanée de disparition : c'est la vitesse moyenne de disparition déterminée sur une durée très petite. Cela correspond à la dérivée par rapport au temps de la quantité de matière du réactif considéré.

$\displaystyle v(t) = \lim_{\Delta t \to 0} \dfrac{\Delta n}{\Delta t} = \dfrac{dn}{dt}$

Pour la déterminer on cherche la pente de la tangente à la courbe $n=f(t)$ au point d'abscisse $t_0$ considérée.

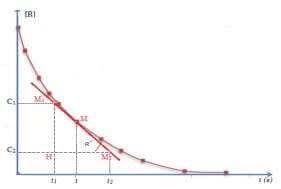
capture-decran-2025-02-28-150514

$\displaystyle v(t) = \tan \alpha' = \dfrac{M_1H}{M_2H} = \dfrac{C_2 - C_1}{t_2 - t_1} = \dfrac{dC}{dt} \bigg]_t$

Relation entre les vitesses de formation et de disparition

Considérons l'équation bilan suivante : $\alpha R_1 + \beta R_2 \longrightarrow \gamma P_1 + \lambda P_2$

$\displaystyle \dfrac{v_d(R_1)}{a} = \dfrac{v_d(R_2)}{b} = \dfrac{v_f(P_1)}{c} = \dfrac{v_f(P_2)}{d}$

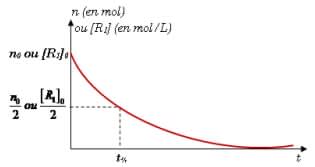
3. Temps demi-réaction

On appelle temps demi-réaction, noté $t_{\frac{1}{2}}$, le temps nécessaire pour que la moitié du réactif en défaut (ou réactif limitant) disparaisse (ou reste). Graphiquement, si on trace la courbe $n=f(t)$ ou $C=f(t)$ pour le réactif limitant : 

capture-decran-2025-02-28-150648

4. Facteurs cinétiques

On appelle facteurs cinétiques les paramètres, tels que la température, la concentration des réactifs et l'utilisation de catalyseurs, qui influent sur la vitesse d'une réaction.

Une transformation chimique est toujours plus rapide quand on augmente la température.