1. Définition et notations
Définition
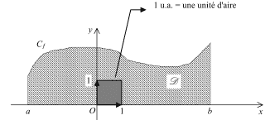
Soit $f$ une fonction continue sur un intervalle fermé borné $\mathrm{I}=[a, b]$, F une primitive quelconque de $f$ sur $\rm I$.
On appelle « intégrale de $a$ à $b$ de $f$ » le réel $\mathrm{F}(b)-\mathrm{F}(a)$ (on montre qu'il est indépendant du choix de $\mathrm F$ et qu'il ne dépend que de la fonction $f$ et des nombres $a$ et $b)$.
Notations et remarques :
- Les réels $a$ et $b$ sont appelés les « bornes » de l'intégrale.
- On note l'intégrale $\displaystyle \int_a^b f(x) d x$.
- Pour écrire l'intégrale, on utilise aussi la notation $\big [\mathrm F(x)\big]_a^b$.
D'où $\displaystyle\int_a^b f(x) d x=\big[\mathrm F(x)\big]_a^b$ $=\mathrm F(b)-\mathrm F(a)$. - Dans la notation $\displaystyle \int_a^b f(x) dx$, on peut remplacer la lettre $x$ par n'importe quelle autre lettre.
Ainsi : $\displaystyle \int_a^b f(x) d x=\displaystyle \int_a^b f(t) dt$. - Si $f$ est une fonction continue sur un intervalle $\rm I$ contenant les réels $a$ et $b$ (avec $b < a$), on pose par convention $\displaystyle \int_a^b f(x) d x=-\int_b^a f(x) d x$
2. Propriétés de l'intégrale
Propriété 1 : Linéarité
Soient $f$ et $g$ deux fonctions numériques définies et continues sur un intervalle $\rm I$ et soient $a$ et $b$ des éléments de $\rm I$.
- Soit $\lambda \in \mathbb{R}$ : $\displaystyle \int_a^b(\lambda f(x)) d x=\lambda \int_a^b f(x) d x$ (1re formule de linéarité).
2. $\displaystyle\int_a^b(f+g)(x) d x=\int_a^b f(x) d x+\int_a^b g(x) d x$ (2nde formule de linéarité).
Il en résulte que $\displaystyle \int_a^b(\lambda f+\mu g)(x) d x=\lambda \int_a^b f(x) d x+\mu \int_a^b g(x) d x$ pour tous réels $\lambda$ et $\mu$.
Propriété 2 : Relation de CHASLES
Soit $f$ une fonction continue sur un intervalle $\rm I$ contenant les réels $a$, $b$ et $c$.
On a alors $\displaystyle \int_a^b f(x) d x=\int_a^c f(x) d x+\int_c^b f(x) d x$.
Propriété 3 : Intégrale et inégalités
Soit $f$ et $g$ deux fonctions continues sur $[a, b]$.
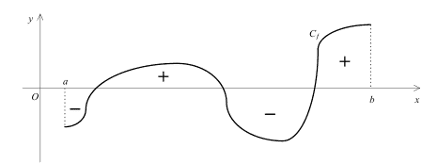
- Positivité : Si, pour tout réel $x$ de $[a, b]$, on a $f(x) \geq 0$, alors $\int_a^b f(x) d x \geq 0$.
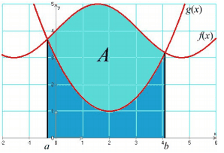
Autrement dit, si $f$ est positive sur $[a, b]$, alors $\displaystyle\int_a^b f(x) d x$ est un réel positif. - Intégration d'une inégalité : Si pour tout réel $x$ appartenent à $[a, b]$, on a $f(x) \leq g(x)$, alors on a : $\displaystyle \int_a^b f(x) d x \leq \int_a^b g(x) d x$
- Inégalités de la moyenne : Si $m$ et $\rm M$ sont deux réels tels que, pour tout réel $x$ appartenant à $[a, b]$, $m \leq f(x) \leq \rm M$, alors on a : $\displaystyle m(b-a) \leq \int_a^b f(x) d x \leq \mathrm M(b-a)$.
Attention : Les résultats de ce théorème ne sont valables qu'avec la condition $\color{orange}{\boldsymbol{a \leq b}}$.
Corollaire 1 (Majoration) : Si $\rm M$ est un réel strictement positif tel que : pour tout réel $x$ appartenant à $[a, b]$, on a : $|f(x)| \leq \rm M$, alors : $\displaystyle \left|\int_a^b f(x) d x\right| \leq \mathrm M|b-a|$.
Corollaire 2 (Comparaison) : Soit $f$, $g$ et $h$ trois fonctions continues sur un intervalle $[a, b]$ et telles que, pour tout $x \in [a, b]$, on ait : $h(x) \leq f(x) \leq g(x)$.
Alors, on a : $\displaystyle \int_a^b h(x) d x \leq \int_a^b f(x) d x \leq \int_a^b g(x) d x$.
Corollaire 3 (Valeur absolue) : Soit $f$ une fonction continue sur $[a, b]$, alors $\displaystyle \left|\int_a^b f(x) d x\right| \leq \int_a^b|f(x)| d x$.
Propriété 4 : Valeur moyenne
Soit $f$ une fonction continue sur $[a,b]$.
La valeur moyenne de $f$ est :
$\displaystyle\frac{1}{b-a}\int_a^b f(x)dx$