Primitives et calcul intégral

1. Primitives

Définition

Soit $F$ une fonction admettant sur un intervalle $\rm I$ une fonction dérivée $f$. On dit que $F$ est une fonction primitive de $f$ sur $\rm I$.

En d'autres termes, $F$ est une primitive de $f$ sur $\rm I$ si et seulement si :

• $F$ est dérivable sur $\rm I$ et, pour tout $x$ de $\rm I$, $F'(x) = f(x)$.

Propriétés

• Si $f$ est dérivable sur $\rm I$ alors $f$ admet des primitives sur $\rm I$.
• Si $f$ admet $F$ comme primitive sur $\rm I$, alors elle en admet une infinité : ce sont toutes les fonctions de la forme $F + C$, où $C$ est une constante arbitraire.
• Si $f$ admet des primitives sur $\rm I$, il en existe une et une seule $G$ qui prend une valeur $b$ en un point donné $a$ de $\rm I$ c'est-à-dire tel que $G(a) = b$.
• Si $F$ est une primitive de $f$ sur $\rm I$, alors $kF$ est une primitive de $kf$ sur $\rm I$.
• Si $F$ est une primitive de $f$ sur $\rm I$ et $G$ une primitive de $g$ sur $\rm I$, alors $F+G$ est une primitive de $f+g$ sur $\rm I$.

Théorèmes

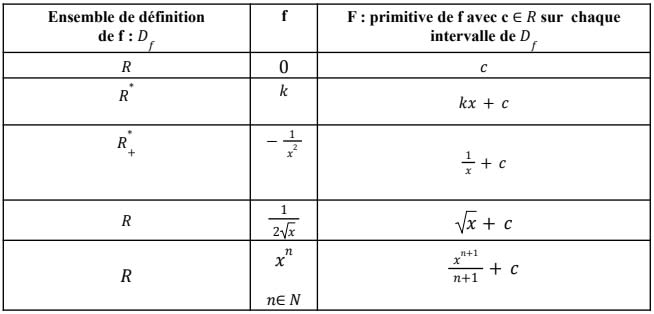
• Primitives usuelles

Voici quelques primitives des fonctions usuelles :

Généralisation

• La fonction $x \longmapsto x^r$, avec $r \in \mathbb{Z} \setminus \{-1\}$, a pour primitives sur $\mathbb{R}^*_+$ les fonctions
  $x \longmapsto \dfrac{x^{r+1}}{r+1} + c$.

• Soit $u$ une fonction dérivable (non nulle si $r<0$) sur un intervalle $\rm I$. Alors la fonction $u \longmapsto u'u^r$, avec $r \in \mathbb{Z} \setminus \{-1\}$, a pour primitives sur $\rm I$ : $\dfrac{u^{r+1}}{r+1} + c$.

Cas particuliers importants

• $\dfrac{u'}{u^2}$ a pour primitives sur $\rm I$ : $-\dfrac{1}{u} + c$ (On prend $r = -1$).
• $\dfrac{u'}{2\sqrt{u}}$ a pour primitives sur $\rm I$ : $\sqrt{u} + c$ (On prend $r = -\dfrac{1}{2}$).

2. Calcul intégral

Théorème

Étant donnée une fonction $f$ dérivable sur un intervalle $\rm I$ et un couple $(a, b)$ de points de $\rm I$, le nombre $F(b) - F(a)$, où $F$ est une primitive de $f$, est indépendant du choix de $F$.

Définition

Soit $f$ une fonction qui admet comme primitive $F$ sur un intervalle $\rm I$ et $(a, b)$ un couple de points de $\rm I$. Le nombre $F(b) - F(a)$ s'appelle intégrale de $a$ à $b$ de $f$ et se note $\displaystyle \int_{a}^{b} f(x) dx$.

Remarques :

• $\displaystyle \int_{a}^{b} f(x) dx$ ne dépend pas du choix de $F$.
• On écrit aussi : $\displaystyle \int_{a}^{b} f(x) dx = [F(x)]_a^b = F(b) - F(a)$

Propriétés

Soit $f$ et $g$ deux fonctions admettant des primitives sur un intervalle $\rm I$ et $a$, $b$, $c$ trois points de $\rm I$.

On a les propriétés suivantes :

• $\displaystyle \int_{a}^{c} f(x) dx + \int_{c}^{b} f(x) dx = \int_{a}^{b} f(x) dx$.
• $\displaystyle \int_{a}^{b} f(x) dx = - \int_{b}^{a} f(x) dx$.
• $k \in \mathbb{R}, \displaystyle \int_{a}^{b} (kf)(x) dx = k \int_{a}^{b} f(x) dx$.
• $\displaystyle \int_{a}^{b} (f + g)(x) dx = \int_{a}^{b} f(x) dx + \int_{a}^{b} g(x) dx$.

Calcul d'aires

Soit $f$ une fonction dérivable sur $[a, b]$, $\mathcal{C}$ sa représentation graphique et $F$ une primitive quelconque de $f$.

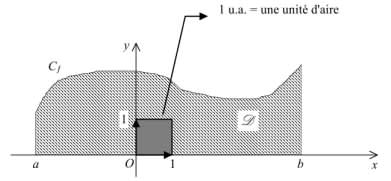
• Unité d'aire

Soit $(\mathrm{O}, \vec{i}, \vec{j})$ un repère orthogonal. On considère les points : $\mathrm{A}(1~;0)$, $\mathrm{B}(0~;1)$ et $\mathrm{C} (1~;1)$.

On convient de prendre pour unité d'aire l'aire du rectangle $\mathrm{OACB}$.

L'unité d'aire, souvent notée $\rm u. a$ est : $1~\rm u. a. = ||\vec{i}|| \cdot ||\vec{j}||$.

• Cas d'une fonction positive

Théorème (admis)

Soit $f$ une fonction continue et positive sur un intervalle $[a, b]$, c'est-à-dire telle que : pour tout réel $x$ appartenant à $[a, b]$, $f(x) \geq 0$.

L'aire $\mathcal{A}$, exprimée en unités d'aire, de l'ensemble $\rm D$ de tous les points dont les coordonnées $(x, y)$ vérifient $a \leq x \leq b$, et $0 \leq y \leq f(x)$ est $\mathcal{A} = \displaystyle \int_{a}^{b} f(x) dx$.

• Cas d'une fonction négative

Théorème (admis)

Soit $f$ une fonction continue et négative sur un intervalle $[a, b]$, c'est-à-dire telle que : pour tout réel $x$ appartenant à $[a, b]$, $f(x) \leq 0$.

L'aire $\mathcal{A}$, exprimée en unités d'aire, de l'ensemble $\rm D$ de tous les points dont les coordonnées $(x, y)$ vérifient $a \leq x \leq b$, et $f(x) \leq y \leq 0$ est $\mathcal{A} = \displaystyle \int_{a}^{b} (-f(x)) dx$.

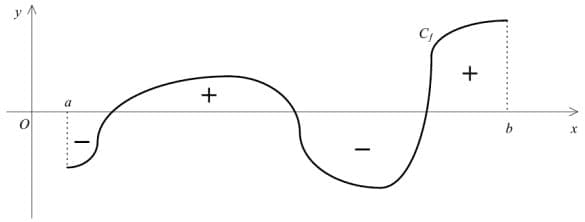
• Cas d'une fonction de signe quelconque

Soit $f$ une fonction continue sur l'intervalle $[a, b]$. $\displaystyle \int_{a}^{b} f(x) dx$ se calcule en comptant positivement l'aire des domaines où $f$ est positive et négativement l'aire des domaines où $f$ est négative.

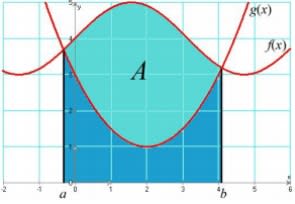
• Aire d'une surface délimitée par deux courbes

Théorème (admis)

Soit $f$ et $g$ deux fonctions continues sur un intervalle $[a, b]$, et telles que : pour tout réel $x$ appartenant à $[a, b]$, $f(x) \leq g(x)$.

L'aire $\mathcal{A}$, exprimée en unités d'aire, de l'ensemble $\rm D$ de tous les points dont les coordonnées $(x, y)$ vérifient $a \leq x \leq b$, et $f(x) \leq y \leq g(x)$ est

$\mathcal{A} = \displaystyle \int_{a}^{b} (g(x) - f(x)) dx$.