1. Calculs sur les limites
Notion de limite
De manière intuitive, la limite d'une fonction décrit ce que ses valeurs deviennent lorsqu'on s'approche d'un certain point $x$, sans nécessairement y arriver.
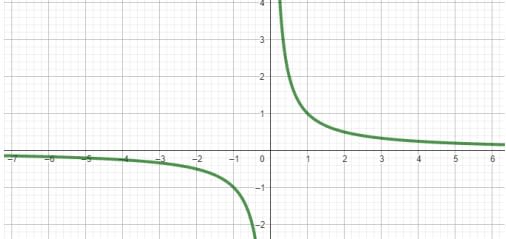
Exemple : Soit $f$ la fonction définie par $f(x) = \dfrac{1}{x}$.
Nous admettons que sa courbe est donnée par la figure ci-dessous :
Plus $x$ devient grand en valeur absolue ($x \to +\infty$ ou $-\infty$), plus $f(x)$ se rapproche de $0$, mais sans jamais l'atteindre.
On dit alors que : La limite de $f(x)$, lorsque $x \to +\infty$, est égale à $0$.
Limites finies en un réel $a$
Du point de vue des calculs, nous admettrons les résultats importants suivants :
- Si $P$ est une fonction polynôme, alors pour tout réel $a$, on a $\displaystyle \lim_{x \to a} P(x) = P(a)$.
- Si $f$ est une fonction rationnelle (rappelons que cela signifie qu'elle est de la forme $f(x) = \dfrac{P(x)}{Q(x)}$, où $P$ et $Q$ sont des polynômes), et si son dénominateur ne s'annule pas en $a$, c'est-à-dire si $Q(a) \neq 0$, alors $\displaystyle \lim_{x \to a} f(x) = \dfrac{P(a)}{Q(a)}$.
Extension de la notion de limite
Rappelons que les symboles $+\infty$ et $-\infty$ ne sont pas des réels. Donc, pas question de faire des opérations sur eux !
Mais lorsqu'on dit que « $x$ tend vers $+\infty$ », cela signifie que $x$ peut être rendu aussi grand qu'on veut. Dire que « $x$ tend vers $-\infty$ » signifie que $x$ peut être rendu aussi petit qu'on veut.
- Limites usuelles
- Limites de la fonction $f : x \to x^n, n \in \mathbb{N}^*$
- Limites de la fonction $f : x \to x^n, n \in \mathbb{N}^*$
| $\displaystyle\lim_{n\to +\infty} x^n=+\infty$ pour tout $n$ |
| $\displaystyle\lim_{n\to +\infty} x^n=+\infty$ pour $n$ pair |
| $\displaystyle\lim_{n\to +\infty} x^n=-\infty$ pour $n$ impair |
-
- Limites de la fonction $f : x \to \dfrac{1}{x^n}, n \in \mathbb{N}^*$
- Limites de la fonction $f : x \to \dfrac{1}{x^n}, n \in \mathbb{N}^*$
| $\displaystyle\lim_{n\to +\infty} \frac{1}{x^n}= 0$ pour tout $n$ |
| $\displaystyle\lim_{n\to +\infty} \frac{1}{x^n}= 0$ pour tout $n$ |
| $\displaystyle\lim_{n\to +\infty} \frac{1}{x^n}= +\infty$ pour $n$ pair |
| $\displaystyle\lim_{n\to +\infty} \frac{1}{x^n}= +\infty$ pour $n$ impair |
$x \to 0^+$ signifie que $x$ se rapproche de 0 par valeurs supérieures à 0.
$x \to 0^-$ signifie que $x$ se rapproche de 0 par valeurs inférieures à 0.
- Limites d'une fonction polynôme
Lorsque $x$ tend vers $+\infty$ ou $-\infty$, une fonction polynôme a même limite que son monôme de plus haut degré.
- Limites d'une fonction rationnelle
Lorsque $x$ tend vers $+\infty$ ou $-\infty$, une fonction rationnelle a même limite que le quotient des monômes de plus haut degré du numérateur et du dénominateur.
Opérations sur les limites
Les résultats suivants sont valables lorsque $x \to a, x \to a^+, x \to a^-, x \to +\infty$ ou $x \to -\infty$.
- Somme de deux fonctions
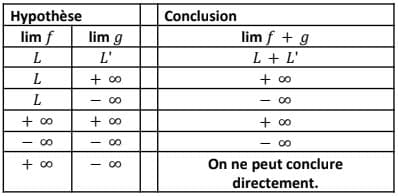
- Produit de deux fonctions
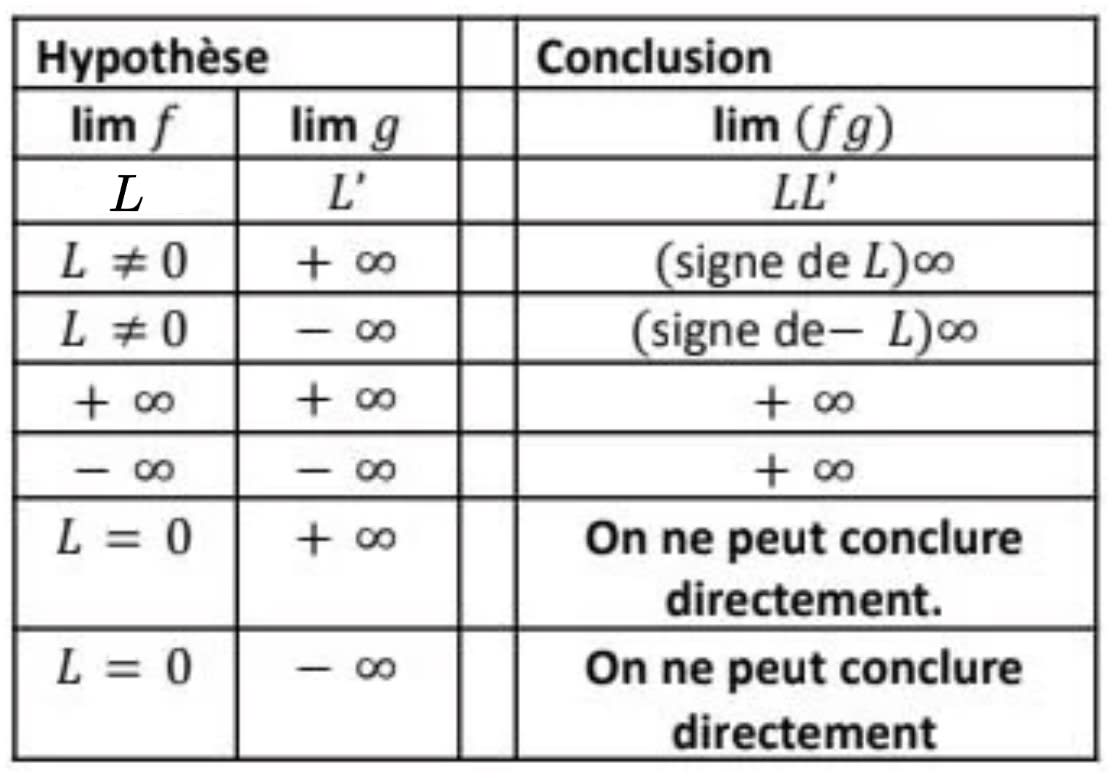
- Inverse et racine carrée d'une fonction
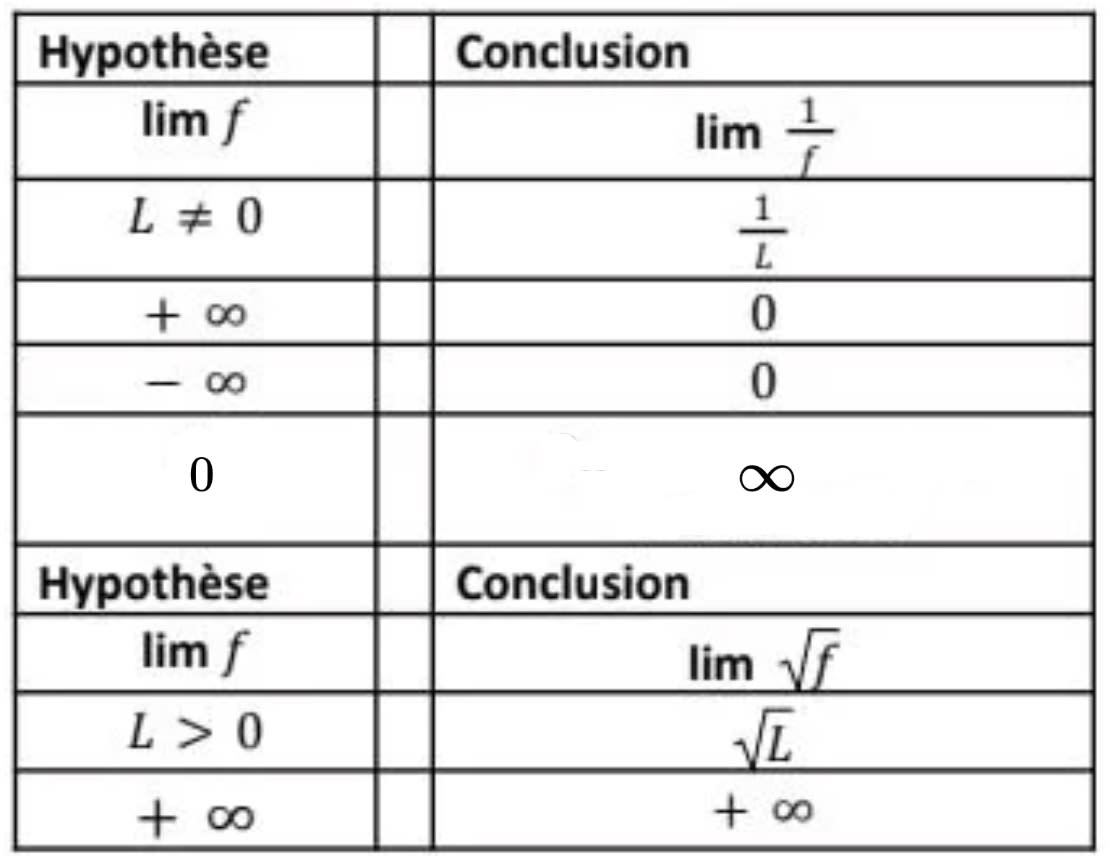
- Quotient de deux fonctions
Soient $f$ et $g$ deux fonctions. Pour obtenir $\displaystyle \lim \dfrac{f}{g}$, on écrit $\dfrac{f}{g} = f \times \dfrac{1}{g}$ et on applique les résultats sur le produit et l'inverse des fonctions.
- Fonction composée
Soient $f$ et $g$ deux fonctions et $a, b, c$ des réels.
Si $\displaystyle\lim_{x\to a}f(x)=b$ et si $\displaystyle \lim_{y\to b}g(y)=c$ alors $\displaystyle\lim_{x\to a} g(f(x))=c$
Ce résultat reste valable si $a$, $b$ et $c$ valent $+\infty$ ou $-\infty$.
2. Notion de continuité
Définition intuitive de la continuité
Une fonction $f$ est dite continue en un point $a$ de son domaine de définition (en général, un intervalle de $\mathbb{R}$), si une des conditions suivantes est satisfaite (les trois conditions sont équivalentes) :
- $f(a)$ existe (i.e. $f$ est définie en $a$).
- $\displaystyle \lim_{x \to a} f(x)$ existe.
- $\displaystyle \lim_{x \to a} f(x) = f(a)$.
Graphiquement, cela se traduit par le fait que l'on peut tracer sa courbe en ce point sans lever le crayon.
Continuité sur un intervalle
Une fonction est continue sur un intervalle $I$ si elle est continue en tout point de cet intervalle. Cela signifie que sa courbe peut être tracée sur tout l'intervalle $I$ sans interruption.
Exemple : Les fonctions usuelles, affines, carré, cube, sont continues sur $\mathbb{R}$ car leurs courbes ne présentent de saut.
On démontre, et nous l'admettrons, que l'image d'un intervalle $I$ par une fonction continue $f$ (c'est-à-dire l'ensemble de tous les nombres $f(x)$, pour $x \in I$), est un intervalle noté $f(I)$.
3. Dérivées
Nombre dérivé et interprétation géométrique
- Définition du nombre dérivé :
Le nombre dérivé de $f$ en un point $a$, noté $f'(a)$, est la limite du taux de variation de $f$ entre $a$ et $a+h$ lorsque $h$ tend vers 0 :
- Interprétation géométrique
- Le nombre dérivé $f'(a)$ représente le coefficient directeur de la tangente à la courbe $y = f(x)$ au point $A(a,f(a))$.
- La tangente est la droite qui « approche au mieux » la courbe en $A$. L'équation de cette tangente est donnée par: $y=f'(a)(x-a)+f(a)$.
Théorèmes sur les fonctions dérivées
- Dérivabilité et continuité :
Si $f$ est dérivable en un point $a$, alors $f$ est continue en $a$.
Cependant, la réciproque est fausse : une fonction continue peut ne pas être dérivable en un point (exemple : la fonction valeur absolue $f : x \to f(x)=|x|$ n'est pas dérivable en $x=0$).
- Dérivée des fonctions usuelles :
On a les formules de dérivation suivantes, résumées dans le tableau ci-dessous :
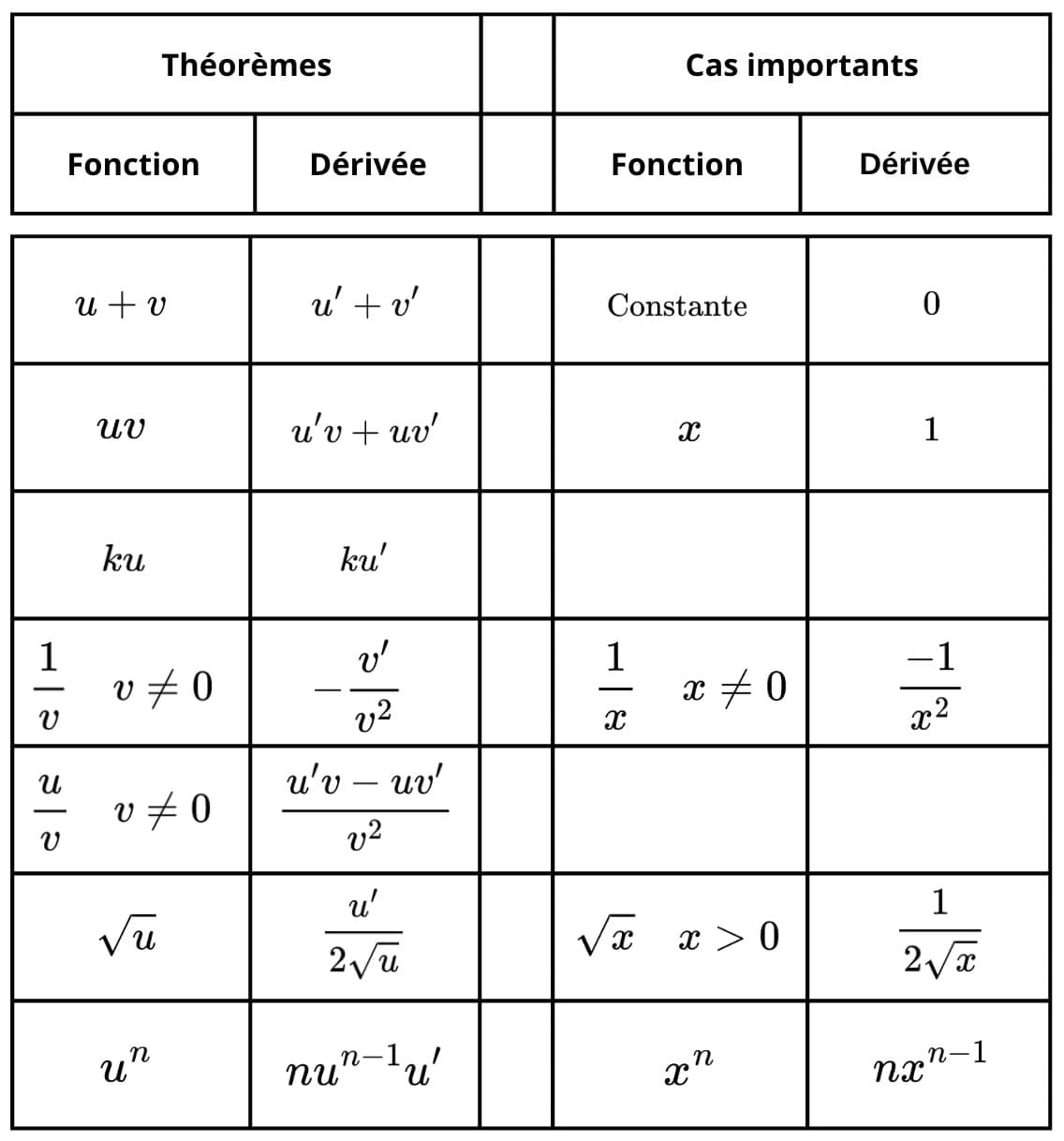
Composée : Si $u(x)$ est dérivable, alors $(f \circ u)'(x) = f'(u(x)) \cdot u'(x)$.
- Dérivées de fonctions du type $g(ax+b)$ et $\dfrac{ax+b}{cx+d}$
Fonction affine composée :
Si $f(x)=g(ax+b)$, où $g$ est dérivable, alors : $f'(x) =a \cdot g'(ax+b) $.
Exemple : Si $f(x) = \sin(2x+3)$, alors $f'(x)= 2 \cos(2x+3)$
Fonction rationnelle :
Si $f(x)= \dfrac{ax+b}{cx+d}$, alors : $\displaystyle f'(x) = \dfrac{(ad-bc)}{(cx+d)^2}$
Exemple : Pour $f(x) = \dfrac{2x+1}{x+3}$, alors $\displaystyle f'(x)= \dfrac{5}{(x+3)^2}$.
- Utilisations de la dérivée
Sens de variation :
La dérivée permet de déterminer les variations d'une fonction :
- Si $f'(x)>0$ sur un intervalle, alors $f$ est croissante sur cet intervalle.
- Si $f'(x)<0$ sur un intervalle, alors $f$ est décroissante sur cet intervalle.
- Si $f'(x)=0$, cela peut correspondre à un extremum (maximum ou minimum).
Équation de la tangente :
L'équation de la tangente à la courbe $y=f(x)$ au point $A(a,f(a))$ est donnée par :
Notion de bijection :
Si $f$ est dérivable et strictement monotone (c'est-à-dire que $f'(x)$ ne change pas de signe), alors $f$ est bijective sur son domaine.
- Si $f$ est croissante, sa bijection réciproque est une fonction croissante.
- Si $f$ est décroissante, sa bijection réciproque est une fonction décroissante.
Exemple : La fonction $f(x) = x^3$ est bijective sur $\mathbb{R}$.