Fonction logarithme népérien

1. Étude de la fonction logarithme népérien

Définition et notation

Nous admettons qu'il existe une seule fonction ayant les propriétés suivantes : 

• elle est définie et dérivable sur $]0, + \infty[$
• elle s'annule en $1$
• elle a pour fonction dérivée la fonction $x \rightarrow \dfrac{1}{x}$

Cette fonction est appelée fonction logarithme népérien et notée $\bf \ln$.

Autrement dit :

• L'ensemble de définition de la fonction $\ln$ est $]0, +\infty[$ et pour tout $x$ appartenant à $]0, +\infty[$, l'image de $x$ par la fonction logarithme népérien est le réel noté $\ln x$.
• $\ln 1 = 0$
• la fonction $\ln$ est dérivable sur $]0, +\infty[$ et, pour tout $x$ strictement positif, $(\ln x)' = \dfrac{1}{x}$

Propriétés

Pour tous réels $a > 0$ et $b > 0$, on a : 

• $\ln (a \times b) = \ln a + \ln b$ (propriété fondamentale)
• $\ln (\dfrac{1}{a}) = -\ln (a)$
• $\ln (\dfrac{a}{b}) = \ln (a) - \ln (b)$
• $\ln (\sqrt{a}) = \dfrac{1}{2} \ln (a)$
• $\ln (a^n) = n \ln (a)$ pour tout entier relatif $n$.

Exemple : Exprimons à l'aide de $\ln 2$ et $\ln 3$, le nombre suivant :
$A = \ln(2 \times 3) + \ln \dfrac{3}{4} - \ln 2^3$

D'après les règles précédentes, $A = \ln 2 + \ln 3 + \ln 3 - \ln 4 - 3 \ln 2 = 2\ln 3-4\ln 2$.

Représentation graphique de $\ln$

• Limites aux bornes

Soit $f$ la fonction définie par $f(x) = \ln x$. On a les résultats suivants, que nous admettrons :

• • $D_f = ]0, + \infty[$
  • $\displaystyle \lim_{x \to 0} \ln x = -\infty$
  • $\displaystyle \lim_{x \to +\infty} \ln x = +\infty$

• Branches paraboliques

Ces limites montrent que la courbe $C_f$ de la fonction logarithme admet pour asymptote verticale la droite d'équation $x=0$ .

On a aussi la limite suivante (admise) : $\displaystyle \lim_{x \to +\infty} \dfrac{f(x)}{x} = \displaystyle \lim_{x \to +\infty} \dfrac{\ln x}{x} = 0$ donc $C_f$ admet une branche parabolique de direction l'axe des abscisses en $+\infty$.

• Tableau de variation

De la définition de la fonction $\ln$, on déduit que : pour tout $x \in ]0~; + \infty[$,
$f'(x) = (\ln)' (x) = \dfrac{1}{x}$.
Or $\dfrac{1}{x} > 0 \text{ sur } ]0~; + \infty[$, donc $f$ est strictement croissante sur $]0~; + \infty[$.

Par conséquent, voici le tableau de variation de ln :

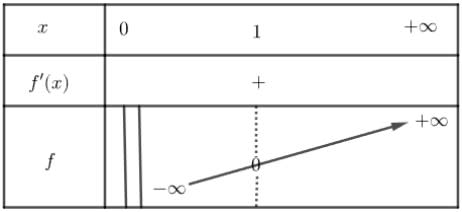
Remarque : Nous admettrons qu'il existe un unique réel noté $e$ tel que $\ln e = 1$ et qu'une valeur approchée de $e$ est $e \approx 2, 718$. On dit que $e$ est la base des logarithmes népériens.

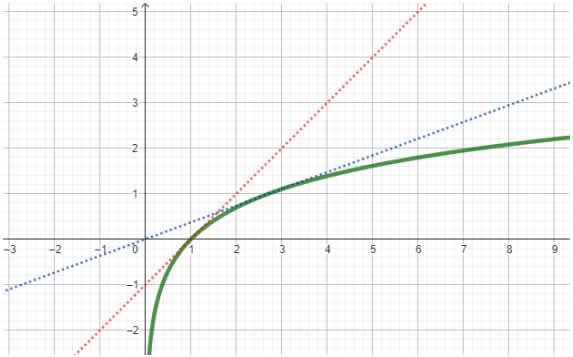
• Courbe représentative de $\ln$
  
  
  • Équations des tangentes aux points d'abscisses 1 et $\rm e$

$\checkmark$ L'équation de la tangente (T) à $C_f$ au point d'abscisse 1 est (T) :
$y = f'(1)(x - 1) + f(1) = x - 1$

$\checkmark$ L'équation de la tangente (T') à $C_e$ au point d'abscisse $e$ est
$(T'): y = f'(e)(x - e) + f(e) = \dfrac{1}{e}(x - e) + 1 = \dfrac{1}{e} x$.

• • Tableau de valeurs

La courbe a l'allure suivante : 

2. Équations et inéquations faisant intervenir $\ln$

Équations

La propriété de base que l'on utilise est la suivante : Pour tous réels $a$ et $b$ strictement positifs, on a : 
$(\ln a = \ln b ) \Leftrightarrow (a = b)$

Pour résoudre une telle équation, on procède ainsi : 

1. On écrit que les quantités dont on prend les logarithmes doivent être strictement positives. Cela se traduit en général par un système d'inéquations.
   
   
2. On résout ce système d'inéquations. L'ensemble des solutions de ce système est appelé domaine de validité de l'équation noté $D_v$.
   
   
3. À l'aide des propriétés de la fonction $\ln$, on transforme l'équation sous la forme $\ln [u(x)] = \ln [v(x)]$. $u$ et $v$ étant des fonctions éventuellement constantes.
   
   
4. En se ramenant à la propriété de base ci-dessus, on résout alors l'équation $u(x) = v(x)$ dans $D_v$.

Exemple : Résolvons dans $\mathbb{R}$ l'équation $\ln (- x + 1) = \ln (2x + 6)$
Pour trouver le domaine, on résout le système d'inéquations $\begin{cases} - x + 1 > 0 \\ 2x + 6 > 0 \end{cases}$, qui est équivalent à $- 3 < x < 1$.
On résout ensuite dans $] - 3; 1[$ l'équation : 
$- x + 1 = 2x + 6$ qui a pour ensemble de solutions $S = \begin{Bmatrix} - \dfrac{5}{3} \end{Bmatrix}$. Ce nombre étant bien dans l'intervalle $] - 3; 1[$, l'unique solution de l'équation proposée est donc $x = - \dfrac{5}{3}$.

$N.B.$ L'équation $\ln x = m$ a pour unique solution $x = e^m$ quel que soit l'entier relatif $m$.

Inéquations

La propriété de stricte croissance de la fonction $\ln$ sur $]0, +\infty[$ entraîne que pour $a > 0$ et $b > 0$, on a : 

• $\ln a \leq \ln b \Leftrightarrow a \leq b$
• $\ln a \geq \ln b \Leftrightarrow a \geq b$.

$N.B.$ Les inégalités larges peuvent être remplacées par des inégalités strictes.

• Inéquations du type $\ln [u(x)] \leq \ln [v(x)]$.

Pour résoudre une telle inéquation, on procède ainsi :

1. On détermine $D_v$ en résolvant le système d'inéquations $\begin{cases} u(x) > 0 \\ v(x) > 0 \end{cases}$.
   
   
2. Dans $D_v$, l'inéquation $\ln [u(x)] \leq \ln [v(x)]$ devient $u(x) \leq v(x)$. On résout alors l'inéquation $u(x) \leq v(x)$ dont l'ensemble de solutions est noté $S_1$. L'ensemble $S$ des solutions de l'inéquation est donné par $S = S_1 \cap D_v$.

• Inéquations du type $\ln [u(x)] \geq \ln [v(x)]$.

On procède de la même manière mais en remplaçant $\leq$ par $\geq$.

$N.B.$ L'inéquation $\ln x \leq m$ a pour unique solution $x \leq e^m$ et l'inéquation $\ln x \geq m$ a pour unique solution $x \geq e^m$ quel que soit l'entier relatif $m$.

3. Fonctions faisant intervenir $\ln$

Limites usuelles

• $\displaystyle \lim_{x \to 0} x \ln x = 0$
• Si $n$ est un entier naturel non nul, alors $\displaystyle \lim_{x \to 0} x^n \ln x = 0$

Ensemble de définition

Soit $u$ une fonction et $f$ la fonction définie par $f(x) = \ln [u(x)]$.
$f(x)$ existe si et seulement si $u(x)$ existe et $u(x) > 0$.

Exemple : Déterminons l'ensemble de définition de la fonction $f$ telle que
$f(x) = \ln \dfrac{x+1}{x-1}$

$f(x)$ existe si et seulement si $\dfrac{x+1}{x-1}$ existe et $\dfrac{x+1}{x-1} > 0$, c'est-à-dire si et seulement si $x \in ]-\infty~; -1[ \cup ]1~; +\infty[$.

Limites de $\ln [u(x)]$

Pour calculer $\displaystyle\lim_{x\to +\infty} \ln [u(x)]$, on calcule d'abord $\displaystyle\lim_{x\to +\infty} [u(x)]$, puis on applique les règles suivantes :

• Si $\displaystyle\lim_{x\to +\infty} [u(x)] = b$, avec $b > 0$, alors $\displaystyle\lim_{x\to +\infty} \ln [u(x)] = \ln b$
• Si $\displaystyle\lim_{x\to +\infty} [u(x)] = 0$, alors $\displaystyle\lim_{x\to +\infty} \ln [u(x)] = -\infty$
• Si $\displaystyle\lim_{x\to +\infty} [u(x)] = +\infty$, alors $\displaystyle\lim_{x\to +\infty} \ln [u(x)] = +\infty$

Exemple : En appliquant ces résultats, on a les limites suivantes :

• $\displaystyle \lim_{x \to +\infty} \ln \dfrac{2x+1}{x-1} = \ln 2$
• $\displaystyle \lim_{x \to +\infty} \ln \dfrac{x+1}{x^2+1} = -\infty$
• $\displaystyle \lim_{x \to +\infty} \ln x^2 = +\infty$

Dérivée

Si $f(x) = \ln [u(x)]$, alors $f'(x) = \dfrac{u'(x)}{u(x)}$