1. Définition et notation

Rappelons que $\ln$ est une fonction strictement croissante et continue sur $]0; + \infty[$. On conçoit alors que, pour tout réel $a$, la droite horizontale d'équation $y = a$ coupe la courbe de $\ln$ en un point unique.

Nous admettons la propriété suivante : « Pour tout nombre réel $a$, l'équation $\displaystyle \ln x = a$ a une solution unique dans ]0; + $\infty$[ ».

capture-decran-2025-02-21-122336

En examinant le graphique de la fonction $\ln$ ci-dessus, on peut s'en convaincre en tenant compte du fait que $\displaystyle \lim_{x \to 0} \ln x = -\infty$ et $\displaystyle \lim_{x \to +\infty} \ln x = +\infty$.

On peut alors considérer la fonction qui, à tout nombre réel $a$, associe l'unique nombre strictement positif $b$ tel que $\displaystyle \ln b = a$. Cette fonction est appelée fonction réciproque de la fonction $\ln$. On la note $\exp$.

$\left\{
\begin{array}{l} b = \exp(a) \\
a \in \mathbb{R} \\
\end{array}
\right.$

$\Leftrightarrow \left
\{\begin{array}{l} a = \ln b\\
b \in ]0; + \infty[
\end{array}
\right.$

2. Propriétés

Conséquences de la définition

  • $\exp(0) = 1$, $\exp(1) = e$
  • Pour tout réel $x$ strictement positif, $\exp(\ln x) = x$
  • Pour tout réel $x$, $\ln(\exp x) = x$

Pour tout réel $x$, on notera désormais $\exp x = e^x$.

Propriétés algébriques

Pour tous réels $a$ et $b$, on a :

  • $\mathrm e^{a+b} = e^a \times e^b$
  • $\mathrm e^{a-b} = \dfrac{e^a}{e^b}$
  • $\mathrm (e^a)^b = (e^b)^a = e^{ab}$

3. Équations et inéquations avec $\exp$

L'équation de base est celle de la forme $\mathrm e^x = m$ ou plus généralement $\mathrm e^{u(x)} = m$, où $u$ est une fonction de $x$. Pour résoudre ce type d'équation, on utilise le logarithme népérien $\ln(x)$, qui est la réciproque de la fonction exponentielle : 

  • $\mathrm e^x = m \Leftrightarrow x = \ln m$ avec $m > 0$
  • $\mathrm e^{u(x)} = m \Leftrightarrow u(x) = \ln m$ avec $m > 0$

Exemple : Soit à résoudre : $\mathrm e^{2x} = 7$. Cela équivaut à : $2x = \ln 7$, d'où $x = \dfrac{\ln 7}{2}$.

Certaines équations plus complexes nécessitent parfois des substitutions pour les rendre plus facile à résoudre.

Exemple : Soit à résoudre : $\mathrm e^x + \mathrm e^{-x} = 3$, on peut poser $y = \mathrm e^x$, et l'équation devient : $y + \dfrac{1}{y} = 3$, qui se ramène à l'équation du second degré : $y^2 - 3y + 1 = 0$. Les solutions de cette équation peuvent être ensuite utilisées pour trouver $x$.

L'inéquation de base est celle de la forme $\mathrm e^x < m$ ou plus généralement $\mathrm e^{u(x)} < m$, où $u$ est une fonction de $x$. Pour résoudre ce type d'équation, on applique le logarithme népérien des deux côtés (car $\ln$ est une fonction croissante) et l'inégalité reste inchangée. :

  • $\mathrm e^x < m \Leftrightarrow x < \ln m$ avec $m > 0$
  • $\mathrm e^{u(x)} < m \Leftrightarrow u(x) < \ln m$ avec $m > 0$

 

Exemple : Soit à résoudre : $\mathrm e^{2x} \geq 4$. Cela équivaut à : $2x \geq \ln 4$, d'où $x \geq \dfrac{\ln 4}{2}$.

L'ensemble des solutions de l'inéquation est donc : $[\dfrac{\ln 4}{2} ; + \infty[$.

On peut rencontrer des situations plus complexes :

Exemple : Soit à résoudre : $e^{2x} + 2e^x - 3 > 0$, on peut poser $y = e^x$, et l'inéquation devient : $y^2 + 2y - 3 > 0$. Cette dernière a pour ensemble de solutions ]$-\infty; -3[ \cup ]1; + \infty[$.

On a donc $e^x < -3$ (ce qui est impossible, car une exponentielle n'est jamais négative) ou bien $e^x > 1$, soit $x > 0$. L'ensemble des solutions de l'inéquation est donc : $]0~; + \infty[$.

4. Limites usuelles

  • $\displaystyle \lim_{x \to -\infty} \mathrm e^x = 0$ ;
  • $\displaystyle \lim_{x \to +\infty} \mathrm e^x = +\infty$ ;
  • $\displaystyle \lim_{x \to -\infty} x\mathrm e^x = 0$ ;
  • $\displaystyle \lim_{x \to +\infty} \dfrac{\mathrm e^x}{x} = +\infty$

Plus généralement pour tout entier naturel non nul $n$, on a : 

  • $\displaystyle \lim_{x \to -\infty} x^n \mathrm e^x = 0$ ;
  • $\displaystyle \lim_{x \to +\infty} \dfrac{\mathrm e^x}{x^n} = +\infty$

5. Étude et représentation graphique de $\exp$

Dérivée

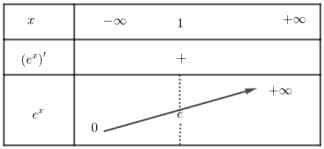
On démontre, et nous l'admettrons, que la fonction exp est dérivable sur $\mathbb{R}$ et que $(e^x)' = e^x > 0$. La fonction exponentielle est strictement croissante sur $\mathbb{R}$.

Tableau de variation

Les résultats précédents et la touche EXP de la calculatrice permettent de donner le tableau de variation de la fonction exp et de construire son graphe.

capture-decran-2025-02-21-122735

Courbe représentative de $\exp$

La courbe a l'allure suivante :

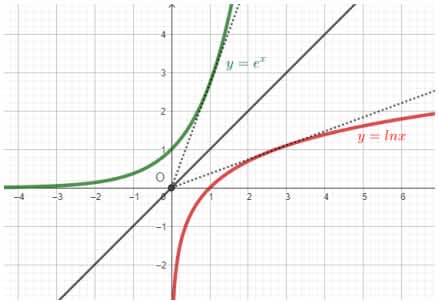
capture-decran-2025-02-21-122817

Tableau de valeurs arrondies

capture-decran-2025-02-21-123000

Remarque : La courbe représentative de la fonction exponentielle et celle de la fonction $\ln$ sont symétriques par rapport à la droite d'équation $y = x$ (première bissectrice des axes) dans un repère orthonormal $(\mathrm{O}, \vec{i}, \vec{j})$.

6. Dérivées de fonctions comportant $\exp$

  • Soit $a$ et $b$ deux réels quelconques avec $a$ non nul. La fonction $x \mapsto \mathrm e^{ax+b}$ est dérivable sur $\mathbb{R}$ et on a : $(\mathrm e^{ax+b})' = a\mathrm e^{ax+b}$
  • Plus généralement, soit $u$ une fonction dérivable sur un intervalle $I$. Alors la fonction composée $\exp u$ est dérivable sur $I$ et on a : $(\mathrm e^u)' = u'\mathrm e^u$