1. Parité et éléments de symétrie
Parité d'une fonction
- Définition
Soit $f$ une fonction définie sur un ensemble $\rm{D}$.
$f$ est paire sur $\rm{D}$ si et seulement si, pour tout $x$ de $\rm{D}$, les deux conditions suivantes sont vérifiées :
1. $(-x) \in \rm{D}$
2. et $f(-x) = f(x)$
$f$ est impaire sur $\rm{D}$ si et seulement si, pour tout $x$ de $\rm{D}$, les deux conditions suivantes sont vérifiées :
1. $(-x) \in \rm{D}$
2. et $f(-x) = -f(x)$.
- Propriétés
Dans un repère orthogonal du plan, la courbe représentative d'une fonction paire est symétrique par rapport à l'axe des ordonnées.
Dans tout repère du plan, la courbe représentative d'une fonction impaire est symétrique par rapport à l'origine du repère.
Éléments de symétrie d'une courbe de fonction
Axe de symétrie parallèle à $(0, \vec{j})$ d'une courbe représentant une fonction
- Propriété
Dans un repère orthogonal, une droite d'équation $x = a$ est un axe de symétrie pour la courbe $(\mathcal{C}_f)$ représentant une fonction $f$, définie sur un ensemble $\mathrm D_f$ si et seulement si les deux conditions suivantes sont vérifiées :
1. Si $x \in \mathrm D_f$, alors $(2a - x) \in \mathrm D_f$
2. et $f(2a - x) = f(x)$
Centre de symétrie d'une courbe représentant une fonction
- Propriété
Dans un repère du plan, un point $\Omega (a, b)$ est un centre de symétrie pour la courbe $(\mathcal{C}_f)$ représentant une fonction $f$, définie sur un ensemble $\mathrm{D}_f$ si et seulement si les deux conditions suivantes sont vérifiées :
1. Si $x \in \mathrm{D}_f$, alors $(2a - x) \in \mathrm{D}_f$
2. et $f(2a - x) + f(x) = 2b$
2. Branches infinies : Asymptotes et Branches Paraboliques
Asymptote « verticale »
Si $\displaystyle \lim_{x \to a^-} f(x) = +\infty$
ou bien $\displaystyle \lim_{x \to a^-} f(x) = -\infty$
ou bien $\displaystyle \lim_{x \to a^+} f(x) = +\infty$
ou bien $\displaystyle \lim_{x \to a^+} f(x) = -\infty$,
alors la droite d'équation $x = a$ est asymptote « verticale » à $(\mathcal{C}_f)$.
Asymptote « horizontale »
Si $\displaystyle \lim_{x \to +\infty} f(x) = b$
ou bien $\displaystyle \lim_{x \to -\infty} f(x) = b$,
alors la droite d'équation $y = b$ est asymptote « horizontale » à $(\mathcal{C}_f)$.
Asymptote « oblique »
La droite d'équation $y = ax + b$ avec $a \neq 0$ est asymptote oblique à $\mathcal{C}_f$ au voisinage de $+\infty$ si $\displaystyle \lim_{x \to +\infty} [f(x) - (ax + b)] = 0$ (de même en $-\infty$).
Dans la pratique, si $f(x) = (ax + b) + \varepsilon(x)$ et si $\displaystyle \lim_{x \to +\infty} \varepsilon(x) = 0$, la droite d'équation $y = ax + b$ est asymptote oblique à $\mathcal{C}_f$ au voisinage de $+\infty$ (de même en $-\infty$).
Le signe de $\varepsilon(x) = f(x) - (ax + b)$ nous renseigne sur la position relative de $\mathcal{C}_f$ et de l'asymptote.
Branches paraboliques
- Si $\displaystyle \lim_{x \to +\infty} \dfrac{f(x)}{x} = 0$ (ou $\displaystyle \lim_{x \to -\infty} \dfrac{f(x)}{x} = 0$), on dit que $\mathcal{C}_f$ admet une branche parabolique de direction l'axe $(0, \vec{i})$.
- Si $\displaystyle \lim_{x \to +\infty} \dfrac{f(x)}{x} = +\infty$ (ou $\displaystyle \lim_{x \to -\infty} \dfrac{f(x)}{x} = -\infty$), on dit que $\mathcal{C}_f$ admet une branche parabolique de direction l'axe $(0, \vec{j})$.
3. Étude d'une fonction
Plan d'étude d'une fonction
Pour étudier et représenter graphiquement les fonctions, on adopte, en général, le plan d'étude suivant :
| 1. Ensemble de définition $\mathrm{D}_f$ | 6. Tableau de variation |
| 2. Ensemble d'étude $\mathrm{E}_f$ | 7. Intersection avec les axes |
| 3. Limites aux bornes de $\mathrm{E}_f$ | 8. Tableau de valeurs |
| 4. Asymptotes et branches infinies | 9. Représentation graphique. |
| 5. Dérivée |
Intersection de deux courbes
L'étude de l'intersection de deux courbes consiste à déterminer les points où elles se rencontrent, c'est-à-dire les points qui appartiennent simultanément aux deux courbes.
Pour y parvenir, dans le cas où les deux courbes soient représentées par : $\mathcal{C}_1 : y = f(x)$ et $\mathcal{C}_2 : y = g(x)$, on peut chercher à résoudre l'équation : $f(x)=g(x)$ (ou, ce qui revient au même, $f(x)-g(x)=0$). On utilise des méthodes adaptées au type de fonction :
- Polynômes : Utiliser des factorisations ou le discriminant.
- Rationnelles : Réduire au même dénominateur et résoudre le numérateur.
- Racines : Isoler la racine et élever au carré (en vérifiant les solutions).
Une fois les valeurs de $x$ trouvées, on calcule les ordonnées correspondantes $y$ en remplaçant chaque solution $x$ dans l'une des expressions $f(x)$ ou $g(x)$.
Interprétation géométrique
Les solutions obtenues donnent les coordonnées des points d'intersection $(x, y)$ des courbes. On peut tracer les courbes et marquer les points trouvés pour visualiser l'intersection.
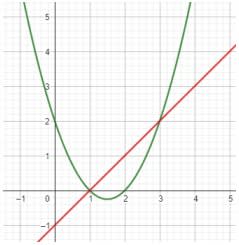
Exemple : Intersection de $f(x)= x^2 - 3x + 2$ et $g(x) = x - 1$