Dans ce qui suit, on ne considère que des ensembles finis, c'est-à-dire des ensembles dont on peut compter les éléments.
On appelle cardinal d'un ensemble fini $\mathrm{A}$ le nombre de ses éléments. Il est noté $\mathrm{Card(A)}$.
Propriétés du cardinal
- $\mathrm{Card} \emptyset = 0$
- Si $\mathrm{A}$ et $\mathrm{B}$ sont des ensembles finis, $\mathrm{Card(A \cup B) = Card(A) + Card(B) – Card(A \cap B)}$.
- $\mathrm{A \times B}$ représentant l'ensemble des couples $(\mathrm{a, b})$ avec $\mathrm{a}$ élément de $\mathrm{A}$ et $\mathrm{b}$ élément de $\mathrm{B}$,
$\mathrm{Card(A \times B) = Card(A) \times Card(B)}$.
P-listes, arrangements et permutations
Définitions
1°) Soit $\mathrm{E}$ un ensemble fini de cardinal $n$. On appelle $p$-liste de $\mathrm{E}$ toute liste ordonnée d'éléments distincts ou non de $\mathrm{E}$.
2°) Soit $\mathrm{E}$ un ensemble fini de cardinal $n$ et $p$ un entier tel que $0 \leq p \leq n$.
On appelle arrangement à $p$ éléments de $\mathrm{E}$ toute $p$-liste d'éléments distincts de $\mathrm{E}$.
On appelle permutation de $\mathrm{E}$ tout arrangement des $n$ éléments de $\mathrm{E}$.
Remarques
- Les listes ordonnées de $p$ éléments pris parmi $n$ avec répétition possible sont appelées $p$-listes.
- Les listes ordonnées de $p$ éléments pris parmi $n$ sans répétition sont appelées arrangements.
Si $p = n$, un arrangement porte le nom de permutation.
Théorèmes
1°) Soit $\mathrm{E}$ un ensemble fini de cardinal $n$. Alors le nombre de $p$-listes de $\mathrm{E}$ est $n^p$.
2°) Soit $\mathrm{E}$ un ensemble fini de cardinal $n$ et $p$ un entier tel que $1 \leq p \leq n$. Alors le nombre d' arrangements à $p$ éléments de $\mathrm{E}$ est le nombre noté :
$\mathrm{A}= n(n - 1) \ldots (n — p + 1)$
(C'est le produit de $p$ entiers consécutifs décroissant à partir de $n$).
Et le nombre de permutations de $\mathrm{E}$ est le nombre noté : $n ! = 1 \times 2 \times \ldots \times n$ (C'est le produit de tous les entiers de 1 jusqu'à $n$).
Combinaisons
Définition
Si $\mathrm{E}$ est un ensemble fini, on appelle combinaison à $p$ éléments de $\mathrm{E}$ tout sous-ensemble de $\mathrm{E}$ de cardinal $p$ ($0 \leq p \leq n$).
Remarque : La combinaison à 0 élément de $\mathrm{E}$ est $\emptyset$.
Théorème
Soit $\mathrm{E}$ un ensemble fini de cardinal $n$. Alors le nombre de combinaisons à $p$ éléments de $\mathrm{E}$ est le nombre noté : $\mathrm{C}_{n}^{p} = \displaystyle \binom{n}{p}= \dfrac{n!}{p!(n-p)!}$.
Propriétés des $\mathrm{C}_{n}^{p}$
- $\mathrm{C}_{n}^{0} = \mathrm{C}_{n}^{n} = 1$
- $\mathrm{C}_{n}^{p} = \mathrm{C}_{n}^{n-p}$
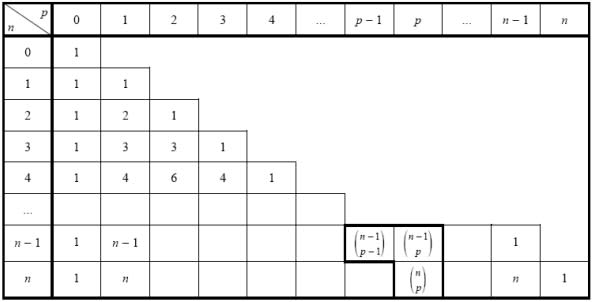
- $\mathrm{C}_{n}^{p} = \mathrm{C}_{n-1}^{p-1} + \mathrm{C}_{n-1}^{p}$. (Formule de Pascal)
Cette dernière formule permet de construire le triangle de Pascal :
Formule du binôme de Newton
Étant donné deux réels $a$ et $b$ et $n$ un entier naturel, on démontre l'égalité :
$(a+b)^n = \displaystyle \sum_{p=0}^{n} \mathrm{C}_{n}^{p} a^{n-p} b^{p}$
$= \mathrm{C}_{n}^{0} a^{n} + \mathrm{C}_{n}^{1} a^{n-1} b + \ldots + \mathrm{C}_{n}^{p} a^{n-p} b^{p} + \ldots + \mathrm{C}_{n}^{n} b^{n}$.