I. Composée d'applications
Définition
- Si $f: \rm{A} \rightarrow \rm{B}$ et $g: \rm{B} \rightarrow \rm{C}$ sont deux fonctions, leur composée est la fonction $h: \rm{A} \rightarrow \rm{C}$ définie par : $h(x) = g(f(x))$.
On note cette composée $h = g \circ f$.
Exemple : Si $f(x) = x^2$ et $g(x) = x + 1$, alors $g \circ f(x) = g(f(x)) = x^2 + 1$.
Décomposition d'une fonction
- Décomposer une fonction consiste à l'écrire comme la composée de deux ou plusieurs fonctions.
Exemple : $h(x) = (x + 2)^3$ peut être décomposée en $f(x) = x + 2$ et $g(x) = x^3$, de sorte que $h(x) = g(f(x))$.
II. Polynômes
Définition
- Un polynôme $P(x)$ est une expression de la forme :
$\displaystyle P(x) = a_n x^n + a_{n-1} x^{n-1} + \dots + a_1 x + a_0$
où les $a_i$ sont des coefficients réels et $n$ est le degré du polynôme.
Méthode de Hörner
- La méthode de Hörner permet de calculer efficacement la valeur d'un polynôme ou de le diviser par un binôme $(x - r)$.
Exemple : Pour $P(x) = 2x^3 - 3x^2 + 4x - 5$, calculons $P(2)$ avec Hörner :
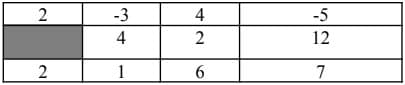
En effet :
- la première ligne du tableau correspond aux coefficients des monômes de $P$.
- pour la deuxième ligne, pour chaque case on multiplie 2 ($a=2$ dans le $P(2)$ cherché) avec la case de la troisième ligne de la colonne précédente (exemple : $12=2\times 6$)
- pour la troisième ligne, pour chaque case, on additionne les cases de la première ligne et de la deuxième ligne de la même colonne (exemple : $6=4+2$).
- la valeur $P(2)$ cherchée correspond à la dernière case du tableau. Ainsi, $P(2) = 7$
Factorisation d'un polynôme
- On cherche à écrire $P(x)$ sous forme de produit de facteurs simples, par exemple $P(x) = (x - r)Q(x)$, où $r$ est une racine de $P(x)$ et $Q(x)$ un polynôme de degré inférieur.
- Utilisation des racines évidentes et du théorème de la racine : $r$ est une racine de $P(x)$ si et seulement si $P(r) = 0$.
Signe d'un polynôme
- Factorisation préalable : pour étudier le signe de $P(x)$, on le factorise en produit de polynômes du premier degré.
- On établit un tableau de signes en prenant en compte :
- Les racines (là où le polynôme s'annule).
- Le degré de chaque facteur (qui détermine le changement ou non de signe).
Exemple : Soit $P(x) = (x - 1)(x + 2)^2 (x - 3)$.
Le tableau de signes est construit autour des racines $-2$, $1$, $3$ en tenant compte de la parité des exposants.


