Voici une proposition de corrigé.
Exercice 1
Question 1
Parmi les $20$ $(= 4 + 6 + 7 + 3)$ boules indiscernables au toucher, $6$ sont violettes.
En tirant une boule au hasard dans l'urne, la probabilité d'obtenir une boule violette est de $\dfrac{6}{20} = \dfrac{3}{10}$.
Proposition C.
Question 2
$70~\%$ correspond à la fraction $\dfrac{70}{100} = 0,70$.
Calculer $70~\%$ d'une quantité revient à multiplier cette quantité par $\dfrac{70}{100} = 0,70$.
Proposition B.
Question 3
L'étendue de cette série est $18 - 7 = 11$.
La moyenne de cette série est $\dfrac{7+18+12+13+15}{5} = \dfrac{65}{5} = 13$.
La médiane de cette série est la 3e des valeurs classées par ordre croissant : c'est $13$.
Proposition D.
Question 4
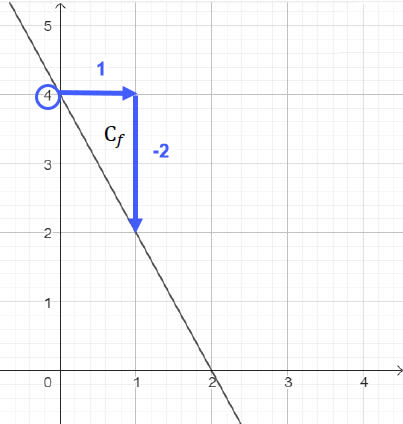
L'ordonnée à l'origine de la courbe de la fonction $f$ est $b = 4$ et son coefficient directeur est $a = -2$.
Elle est donc définie par $f(x) = -2x + 4$.
Proposition C.
Exercice 2
1. Dans le triangle $\rm CDE$ rectangle en $\rm D$, d'après le théorème de Pythagore, on a :
${\rm CE}^2 = {\rm CD}^2 + {\rm DE}^2$
donc
${\rm DE}^2 = {\rm CE}^2 - {\rm CD}^2$$= 29,1^2 - 21,6^2$$= 846,81 - 466,56 = 380,25$.
On a donc : $\rm DE = \sqrt{380,25} = 19,5\:cm.$
2. Dans le triangle $\rm CDE$ rectangle en $\rm D$, le côté $[\rm CD]$ est une base et le côté $[\rm DE]$ la hauteur associée.
L'aire du triangle $\rm CDE$ est donc :
$A_{\rm CDE} = \dfrac{\rm CD \times DE}{2}$$= \dfrac{21,6 \times 19,5}{2}$$= \dfrac{421,2}{2} = 210,6\:{\rm cm}^2.$
3. On considère les triangles $\rm CDE$ et $\rm CFG$.
Les points $\rm G$, $\rm C$ et $\rm E$ sont alignés dans cet ordre, et les points $\rm F$, $\rm C$ et $\rm D$ sont aussi alignés dans cet ordre.
De plus, les droites $(\rm GF)$ et $(\rm DE)$ sont parallèles.
D'après le théorème de Thalès dont les conditions sont vérifiées, on a :
$\dfrac{\rm CD}{\rm CF} = \dfrac{\rm CE}{\rm CG}$$= \dfrac{\rm DE}{\rm FG}$ donc en particulier $\dfrac{\rm CD}{\rm CF} = \dfrac{\rm DE}{\rm FG}$.
Avec les valeurs numériques :
$\dfrac{21,6}{17,2} = \dfrac{19,5}{\rm GF}.$
En utilisant l'égalité des produits en croix :
$21,6 \times \rm GF = 17,2 \times 19,5 = 335,4$, puis $\rm GF = \dfrac{335,4}{21,6} \approx 15,2\:cm$, au $\rm mm$ près.
4. a. $\dfrac{1}{9} \times \rm Aire_{CDE} = \dfrac{210,6}{9} = 23,4 = \rm Aire_{ABC}$, d'après la question 2.
L'aire du triangle $\rm ABC$ est égale à $\dfrac{1}{9}$ de l'aire du triangle $\rm CDE$.
4. b. $\dfrac{1}{9} = \left(\dfrac{1}{3}\right)^2$ et, une réduction de rapport $k$ multipliant les aires par $k^2$, le triangle $\rm ABC$ est une réduction de rapport $\dfrac{1}{3}$ du triangle $\rm CDE$.
Le côté $[\rm AB]$ du triangle $\rm ABC$ étant homologue au côté $[\rm DE]$ du triangle $\rm CDE$, on a :
$\rm AB = \dfrac{DE}{3}= \dfrac{19,5}{3} = 6,5\:\rm cm$.
Exercice 3
Partie A
1. Le périmètre du carré $\rm EFGH$ de côté $2x$ est $P = 4 \times 2x = 8x = 8 \times 1,5 = 12\:{\rm cm}$ car $x = 1,5\:{\rm cm}.$
2. $x = 1,5\:{\rm cm}$, donc $\mathrm {AB} = 16 - 2x = 16 - 2 \times 1,5 = 16 - 3 = 13\:cm.$
3. Il s'agit de construire un rectangle $\rm ABCD$ de longueur $13\:{\rm cm}$ et de largeur $1,5\:{\rm cm}$.
Le plus simple est de le construire à la règle graduée et à l'équerre, en commençant par un côté mesurant $13\:{\rm cm}$, puis les $2$ côtés mesurant $1,5\:{\rm cm}$ à l'aide de l'équerre et de la règle graduée. On trace ensuite le 2e côté mesurant $\rm 13~ cm$.
4. Le périmètre du rectangle $\rm ABCD$ de longueur $L = 13\:{\rm cm}$ et de largeur $l = 1,5\:{\rm cm}$ est :
$P' = 2 \times (L + l) = 2 \times (13 + 1,5) = 2 \times 14,5 = 29\:{\rm cm}$.
D'après la question 1., les périmètres du rectangle $\rm ABCD$ et du carré $\rm EFGH$ ne sont pas égaux, car celui du carré $\rm EFGH$ est $P = 12\:{\rm cm}.$
Partie B
1. a. La formule que l'on a pu saisir dans la cellule $\rm B2$ et que l'on a étiré jusqu'à la cellule $\rm G2$ est :
« $= 8*\rm B1$ ».
1. b. Ce tableau ne nous permet pas de trouver une valeur $x$ pour laquelle les deux périmètres sont égaux car, pour chacune des colonnes $\rm B$ à $\rm G$, la valeur de la ligne $2$ n'est égale à la valeur de ligne $3$.
2. a. Dans le cas général, le périmètre du rectangle $\rm ABCD$ de longueur $L = 16 - 2x$ (en $\rm cm$) et de largeur $l = x$ (en $\rm cm$) est :
$P' = 2 \times (L + l) = 2 \times (16 - 2x + x) = 2 \times (16 - x) = 32 - 2x = -2x + 32.$
2. b. Pour que les périmètres du rectangle $\rm ABCD$ et du carré $\rm EFGH$ soient égaux, il faut que :
$-2x + 32 = 8x$, donc que $8x + 2x = 32$, puis que $10x = 32$ et $x = \dfrac{32}{10} = 3,2\:{\rm cm}.$
Exercice 4
Partie A
1. Le script complété pour dessiner le triangle équilatéral de côté $50$ pas est :
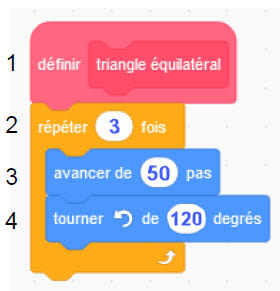
2. Le programme $\rm A$ dessine l'hexagone et le programme $\rm B$ dessine l'autre figure.
En effet, chacun des $6$ triangles équilatéraux de l'hexagone est obtenu à partir du précédent par une rotation d'angle $60°$ dans le sens inverse des aiguilles d'une montre (programme $\rm A$).
Dans le programme $\rm B$, la rotation de $120°$ dans le sens inverse des aiguilles d'une montre fait dessiner deux figures qui se superposent, composées chacune de trois triangles équilatéraux.
Partie B
Il faut répéter la boucle $\rm A = 6$ fois car l'hexagone a $6$ côtés et compléter la boucle par la suite des $2$ instructions suivantes :
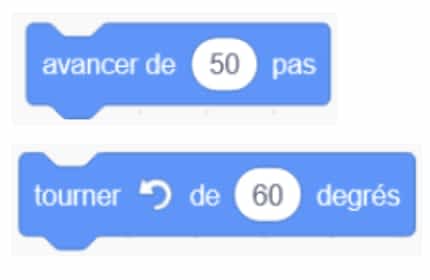
Exercice 5
Partie A
1. $300 = 2 \times 150 = 2 \times 2 \times 75 = 2 \times 2 \times 3 \times 25 = 2 \times 2 \times 3 \times 5 \times 5 = 2^2 \times 3 \times 5^2$.
La décomposition en produit de facteurs premiers de $300$ est $300 = 2^2 \times 3 \times 5^2$. Proposition 3.
2. $350 = 2 \times 175 = 2 \times 5 \times 35 = 2 \times 5 \times 5 \times 7 = 2 \times 5^2 \times 7$.
La décomposition en produit de facteurs premiers de $350$ est $350 = 2 \times 5^2 \times 7$.
3. Le nombre de lots maximal que la responsable du magasin peut constituer est le plus grand des diviseurs communs à $300$ et à $350$.
En observant les deux décompositions en produits de facteurs premiers, c'est $2 \times 5^2 = 50$.
4. Dans chacun des $50$ lots, il y aura $\dfrac{350}{50} = 7$ poissons de type $\rm A$ et $\dfrac{300}{50} = 6$ poissons de type $\rm B$.
Partie B
1.
$\bullet$ Le volume d'eau de l'aquarium $1$, de forme cylindrique et rempli au $\dfrac{4}{5}$, est :
$V_1 = \dfrac{4}{5} \times \pi \times 15^2 \times 25 = \dfrac{4}{5} \times 225 \times 25 \times \pi = 4\,500\pi \approx 14\,130\:{\rm cm}^3 \approx 14,13\:{\rm dm}^3 \approx 14,13\:{\rm L}$ car
$r = \dfrac{30}{2} = 15\:{\rm cm}$ et $1\:{\rm dm}^3 = 1\:{\rm L}$.
$\bullet$ Le volume d'eau de l'aquarium $2$, en forme de pavé droit et rempli au $\dfrac{4}{5}$, est :
$V_2 = \dfrac{4}{5} \times 28 \times 28 \times 30 = \dfrac{4}{5} \times 23\,520 = 18\,816\:{\rm cm}^3 = 18,816\:{\rm dm}^3 = 18,816\:{\rm L}$ car $1\:{\rm dm}^3 = 1\:{\rm L}$.
$\bullet$ Comme il faut prévoir $15\:{\rm L}$ d'eau pour un « poisson combattant », il faut choisir l'aquarium $2$ pour lui.
2. Avant réduction, le prix à payer pour l'achat du « poisson combattant » et de l'aquarium est :
$15 + 40 = 55\:€$.
Le vendeur faisant une réduction de $15~\%$ sur le prix total, la famille va payer $85~\%$ de ce prix, c'est-à-dire :
$\dfrac{85}{100} \times 55 = \dfrac{85 \times 55}{100} = \dfrac{4\,675}{100} = 46,75\:€.$