Exercice 1
Situation 1
Parmi les $40$ boules indiscernables de l'urne, $20$ sont vertes.
En tirant une boule au hasard dans l'urne, la probabilité d'obtenir une boule verte est donc de $\dfrac{20}{40} = \dfrac{1}{2}.$
Situation 2
Décomposons $1~050$ en produit de facteurs premiers en le divisant successivement, et éventuellement plusieurs fois, par les nombres premiers successifs $2$, $3$, $5$, $7$, etc.
$1~050 =2 \times 525=2 \times 3 \times 175=2 \times 3 \times 5 \times 35=2 \times 3 \times 5 \times 5 \times 7=2 \times 3 \times 5^{2} \times 7.$
La décomposition en produits de facteurs premiers de $1~050$ est $1~050 = 2 \times 3 \times 5^{2} \times 7.$
Situation 3
Le montant de l'augmentation de cet article est de : $\dfrac{14}{100} \times 25 = \dfrac{14 \times 25}{100} = \dfrac{14}{4} =3,50~\rm{€}.$
Le prix de cet article de $25~\rm €$ après une augmentation de $14~\%$ est de : $25 + 3,50 = 28,50 ~\rm{€}.$
Situation 4
Un agrandissement de rapport $2,5$ multiplie les aires par $2,5^{2}.$
L'aire du polygone $1$ étant de $7,5~\rm{cm}^{2}$, l'aire du polygone $2$ est donc de $7,5 \times 2,5^{2} = 46,875~ \rm{cm}^{2}$.
Situation 5
1. La moyenne des tailles des élèves de cette classe est de :
$\dfrac{2 \times 152+4 \times 157+2 \times 160+5 \times 162+2 \times 165+4 \times 170+6 \times 174+5 \times 180}{2+4+2+5+2+4+6+5}$
$= \dfrac{5 \ 016}{30}$
$= 167,20~\rm{cm}.$
2. Il y a 30 élèves dans cette classe et $\dfrac{30}{2} = 15$, donc la médiane des tailles est la moyenne de la $15^{\rm{e}}$ et
de la $16^{\rm{e}}$ de ces valeurs classées par ordre croissant.
En lisant dans le tableau, la $15^{\rm{e}}$ de ces valeurs classées par ordre croissant est 165 $\rm{cm}$ et la $16^{\rm{e}}$ de ces
valeurs classées par ordre croissant est $170~\rm{cm}$.
La médiane des tailles des élèves de la classe est donc : $\dfrac{165+170}{2} = \dfrac{335}{2} = 167,50~\rm{cm}$.
Exercice 2
1. Dans le triangle $\rm{ABC}$ rectangle en $\rm{B}$, d'après le théorème de Pythagore, on a :
$\rm{AC}^{2} = \rm{AB}^{2} + \rm{BC}^{2}$, donc $50^{2} = \rm{AB}^{2} + 30^{2}$ puis $\rm{AB}^{2} = 50^{2} – 30^{2} = 2500 - 900 = 1 \ 600$.
On a donc : $\rm{AB} = \sqrt{1 \ 600} = 40~ \rm{m}$.
2. Les droites $\rm (DE)$ et $\rm (BC)$ sont toutes les deux perpendiculaires à la droite $\rm (EB).$
Or, si deux droites sont perpendiculaires à une même droite, alors elles sont parallèles entre elles.
Les droites $\rm (DE)$ et $\rm (BC)$ sont donc parallèles.
3. On considère les triangles $\rm{ABC}$ et $\rm{AED}$.
Les points $\rm{E}$, $\rm{A}$ et $\rm{B}$ sont alignés dans cet ordre, et les points $\rm{D}$, $\rm{A}$ et $\rm{C}$ sont aussi alignés dans cet ordre.
D'après la question précédente, les droites $\rm (DE)$ et $\rm (BC)$ sont parallèles.
D'après le théorème de Thalès, on a :
$\dfrac{\rm{AE}}{\rm{AB}} = \dfrac{\rm{AD}}{\rm{AC}} = \dfrac{\rm{DE}}{\rm{BC}}$ donc en particulier $\dfrac{\rm{AD}}{\rm{AC}} = \dfrac{\rm{DE}}{\rm{BC}}$.
Avec les valeurs numériques : $\dfrac{70}{50} = \dfrac{\rm {DE}}{30}$
En utilisant l'égalité des produits en croix : $50 \times \rm{DE} = 30 \times 70 = 2 \ 100$, puis $\rm{DE} = \dfrac{2 \ 100}{50} = 42 ~\rm{m}$.
4. Dans le triangle $\rm{DEM}$ rectangle en $\rm{E}$, on a : $\tan(\rm{\widehat{DME}}) = \dfrac{\rm{DE}}{\rm{EM}}$.
Avec les valeurs numériques :
$\tan(60^{\circ}) = \dfrac{42}{\rm{EM}}$ donc $\rm{EM} \times \tan(60^{\circ}) = 42$ et $\rm{EM} = \dfrac{42}{\tan(60^{\circ})} \approx 24,2 ~\rm{m}$ au dixième près.
5. Dans le triangle $\rm{AMD}$, $\rm [AM]$ est une base et $\rm [DE]$ la hauteur associée.
Calculons la longueur $\rm{AM}$, après avoir calculé la longueur $\rm{AE}$.
En reprenant l'égalité des quotients suivante $\dfrac{\rm{AE}}{\rm{AB}} = \dfrac{\rm{AD}}{\rm{AC}} = \dfrac{\rm{DE}}{\rm{BC}}$, on a en particulier $\dfrac{\rm{AE}}{\rm{AB}} = \dfrac{\rm{AD}}{\rm{AC}}$.
Avec les valeurs numériques : $\dfrac{\rm{AE}}{40} = \dfrac{70}{50}$.
En utilisant l'égalité des produits en croix : $50 \times \rm{AE} = 40 \times 70 = 2 \ 800$, puis $\rm{AE} = \dfrac{2 \ 800}{50} = 56 ~\rm{m}$.
On en déduit : $\rm{AM} = \rm{AE} – \rm{EM} \approx 56 – 24,2 \approx 31,8~ \rm{m}$ au dixième près.
L'aire du triangle $\rm{AMD}$ est donc :
$\displaystyle A_{\rm{AMD}} = \dfrac{\rm{AM} \times \rm{DE}}{2} \approx \dfrac{31,8 \times 42}{2} \approx 31,8 \times 21 \approx 667,8 ~\rm{m}^{2}.$
Exercice 3
1. Avec le programme $\rm A$, en choisissant $4$ comme nombre de départ, on obtient successivement :
$4 \times 3=12$ ; $12+15= 27$ ; $27 \div 3=9$ ; $9-4= 5$.
Le résultat obtenu est bien $5$.
2. Avec le programme $\rm A$, en choisissant $-2$ comme nombre de départ, on obtient successivement :
$(-2) \times 3 = -6$ ; $-6 + 15 = 9$ ; $9 \div 3 = 3$ ; $3-(-2) = 3+ 2 = 5$.
Le résultat obtenu est bien $5$.
3. Avec le programme $\rm A$, en notant $x$ le nombre de départ, on obtient successivement :
$x \times 3 = 3x$ ; $3x+15$ ; $(3x+15) \div 3=x+5$ ; $x+5 -x = 5$.
Le résultat obtenu est $5$.
Quel que soit le nombre de départ choisi, le résultat est toujours $5$.
L'affirmation « Le programme A donne toujours le même résultat » est donc vraie.
4. Avec le programme $\rm B$, en choisissant $10$ comme nombre de départ, on obtient successivement :
$10-1=9$ et $10-6=4$ ; $9 \times 4=36$ ; $36+5 = 41$.
Le résultat obtenu est $41$.
5. Avec le programme $\rm B$, en notant $x$ le nombre de départ, on obtient successivement :
$x-1$ et $x-6$ ; $(x - 1)(x-6)$ ; $(x-1)(x-6) + 5$.
L'expression du résultat est $(x - 1)(x-6) + 5$.
Étant donné que le programme $\rm A$ donne toujours $5$ comme résultat, on cherche deux valeurs telles que
$(x-1)(x-6) + 5 = 5$ donc que $(x – 1)(x – 6) = 0$ , qui est une équation produit.
On doit donc avoir $x - 1 = 0$ ou $x – 6 = 0$, c'est-à-dire $x = 1$ ou $x = 6.$
Les deux nombres de départ pour lesquels les programmes $\rm A$ et $\rm B$ retournent le même résultat sont $1$ et $6$.
Exercice 4
1. La distance parcourue par Malo n'est pas proportionnelle au temps de parcours, car la représentation graphique de la situation n'est pas une droite (qui passe par l'origine du repère).
2. Au bout de $20$ minutes, Malo a parcouru environ $4,5~\rm{km}$ (voir graphique ci-dessous).
3. Pour faire les $9$ premiers kilomètres, Malo a mis environ $50$ minutes (voir graphique ci-dessous).
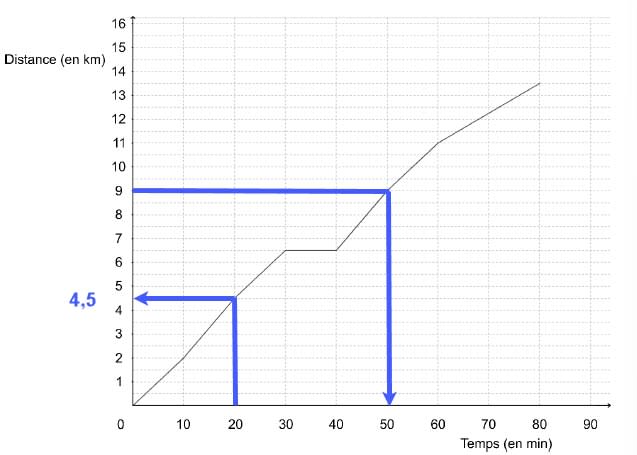
4. Pour faire cette course de distance $d = 13, 5 ~\rm{km}$, Malo a mis le temps :
$t = 80 ~\rm{min} =1 ~\rm{h} \ 20 ~\rm{min} = 1 \rm{h} + \dfrac{20}{60} \rm{h} = 1 ~\rm{h} + \dfrac{1}{3} ~\rm{h} = \dfrac{4}{3} ~\rm{h}$, car $1 ~\rm{h} = 60 ~\rm{min}$.
Sa vitesse moyenne sur cette course est donc :
$\displaystyle v = \dfrac{d}{t} = \dfrac{13,5}{\frac{4}{3}} = \dfrac{13,5 \times 3}{4} = \dfrac{40,5}{4} = 10,125~ \rm{km/h} \approx 10,1 ~\rm{km/h}$ au dixième près.
5. a. Louise et Hillal ont fait la même course, en partant en même temps, mais la vitesse moyenne de Louise a été plus élevée que celle de Hillal.
Entre Louise et Hillal, c'est donc Louise qui a franchi la ligne d'arrivée en premier.
5. b. Calculons le temps au bout duquel Louise a effectué la course, pour ensuite calculer la distance parcourue par Hillal à cet instant :
$\displaystyle v = \dfrac{d}{t}$ donc $\displaystyle t = \dfrac{13,5}{12} = 1,125 ~\rm{h}$.
Calculons la distance parcourue par Hillal au bout de ce temps (en heures décimales) de course :
$\displaystyle v = \dfrac{d}{t}$ donc $d = v \times t = 10 \times 1,125 = 11,25 ~\rm{km}.$
Lorsque Louise passe la ligne d'arrivée, la distance qui la sépare de Hillal est de : $13,5- 11,25 = 2,25~ \rm{km}.$
Exercice 5
1. Le script $1$ permet d'obtenir le dessin $2$ (triangle) et le script $2$ permet d'obtenir le dessin $1$ (hexagone).
Le nombre de répétitions dans le script correspond au nombre de côtés de la figure.
2. Dans la partie qui est répétée deux fois du script $3$, après la consigne « avancer de 30 pas », il manque les consignes suivantes dans cet ordre :
- Instruction B :

- Instruction C :

- Instruction A :

Cet ensemble de 4 consignes permet de tracer la moitié du losange et est donc répétée deux fois, après avoir orienté convenablement le crayon.
3. Les coordonnées du point de départ du lutin sont $(-200~; 0).$
4. Les deux seules captures d'écran possibles sont la n°2 et la nº 3.
Dans le premier cas, $6$ losanges sont dessinés à l'horizontale séparés de $60 – 30 = 30$ pas avec le message affiché
« Voici le dessin ! », et dans le deuxième cas, c'est « Perdu ! » qui est affiché.
5. Pami les nombres $1$, $2$ ou $3$, il faut que $3$ soit choisi (de façon équiprobable) pour que le message affiché soit « Voici le dessin ! ».
La probabilité recherchée est donc de $\dfrac{1}{3}$.
6. a. Dans cette expérience aléatoire, la fréquence de l'affichage du message « Voici le dessin ! » est de :
$\dfrac{40}{40+60} = \dfrac{40}{100} = 0,4$.
6. b. $\dfrac{1}{3} \neq 0,4$ donc la fréquence de l'évènement dans cette expérience aléatoire est différente de sa probabilité.
C'est normal car la probabilité d'un évènement est un résultat théorique attendu, alors que la fréquence de cet évènement est un résultat obtenu lors d'une expérience aléatoire parmi d'autres.
En lançant un plus grand nombre de fois ce programme, la fréquence de l'évènement s'approcherait de sa probabilité théorique.