Voici une proposition de corrigé.
Exercice 1
Question 1
Décomposons $120$ en produit de facteurs premiers en le divisant successivement, et éventuellement plusieurs fois, par les nombres premiers successifs $2$, $3$, $5$, $7$, etc.
$120 = 2 \times 60 = 2 \times 2 \times 30 = 2 \times 2 \times 2 \times 15 = 2 \times 2 \times 2 \times 3 \times 5 = 2^3 \times 3 \times 5$.
La décomposition en produits de facteurs premiers de $120$ est $120 = 2^3 \times 3 \times 5$. Réponse C.
Remarque : les autres propositions, soit ne sont pas un produit de facteurs premiers (réponses A et B), soit ne sont même pas un produit (réponse D).
Question 2
Le nombre affiché dans la cellule B2 est le nombre « $-4 \times \rm{B1} - 12$ ».
Comme la cellule B1 contient le nombre $5$, le nombre affiché dans la cellule B2 est :
$-4 \times 5 - 12 = -20 - 12 = -32$. Réponse A.
Question 3
Les carrés A et B sont du même côté du point O, donc le rapport de l'homothétie est positif.
On voit que le côté du carré B est deux fois plus long que le côté du carré A, donc le rapport de l'homothétie est $2$, comme celui de l'agrandissement du carré A pour obtenir le carré B.
Réponse D.
Question 4
En utilisant l'identité remarquable $a^2 - b^2 = (a - b)(a + b)$ :
$4x^2 - 1 = (2x)^2 - 1^2 = (2x - 1)(2x + 1).$
Réponse A.
Question 5
Dans le triangle $\rm{TER}$ rectangle en $\rm{R}$, on a : $\cos \widehat{\rm{RET}} = \dfrac{\rm{ER}}{\rm{ET}}$.
Avec les valeurs numériques : $\cos(39°) = \dfrac{\rm{ER}}{7,4}$ donc $\rm{ER} = 7,4 \times \cos (39°) \approx 5,75 ~\rm{cm}$ au centième près.
Réponse B.
Exercice 2
1. La moyenne des masses (en $\rm{kg}$) de ces $5$ colis est :
$M = \dfrac{4+9+2+7+11}{5} = \dfrac{33}{5}$$= 6,6 ~\rm{kg}$.
2. $\dfrac{5}{2} = 2,5$ donc la médiane des masses de ces $5$ colis est la $3^{\rm{ième}}$ masse classée par ordre croissant $(2 < 4 < 7 < 9 < 11)$ : c'est $7 ~\rm{kg}$.
Parmi ces $5$ colis, il y a autant de colis qui pèsent moins de $7 ~\rm{kg}$ que de colis qu'y pèsent plus de $7 ~\rm{kg}$.
3. La probabilité que le transporteur choisisse un colis dont la masse est inférieure à $8 ~\rm{kg}$ est de $\dfrac{3}{5}$.
En pourcentage, elle est de :
$\dfrac{3}{5} \times 100 = \dfrac{3 \times 100}{5}~$$= 3 \times \dfrac{100}{5} = 3 \times 20$$= 60~\%$.
4. a. Le volume du colis E est :
$V_{\rm{E}} = L \times l \times h$$= 0,5 \times 0,4 \times 0,6 = 0,12 ~\rm{m}^3$.
4. b. La masse volumique du colis E est :
$\rho = \dfrac{\text{masse (en kg)}}{\text{volume (en m}^3\text{)}}$$= \dfrac{11}{0,12} \approx 91,7 ~\rm{kg/m}^3$ au dixième près.
4. c. La masse volumique du colis C est :
$\rho' = \dfrac{\text{masse (en kg)}}{\text{volume (en m}^3\text{)}} = \dfrac{2}{0,3 \times 0,1 \times 0,5}$$= \dfrac{2}{0,015} \approx 133,3 ~\rm{kg/m}^3$ au dixième près.
Le colis E est plus lourd que le colis C, mais sa masse volumique est plus petite que celle du colis C.
Le transporteur a donc tort.
Exercice 3
1. Avec ce programme, en choisissant $1$ comme nombre de départ, on obtient successivement :
$1 \times (-2) = -2$ ; $-2 + 4 = 2$ ; $2 \times 4 = 8$.
Le résultat obtenu est bien $8$.
2. Avec ce programme, en choisissant $-2$ comme nombre de départ, on obtient successivement :
$(-2) \times (-2) = 4$ ; $4 + 4 = 8$ ; $8 \times 4 = 32$.
Le résultat obtenu est $32$.
3. Avec ce programme, en notant $x$ le nombre de départ, on obtient successivement :
$x \times (-2) = -2x$ ; $-2x + 4$ ; $(-2x + 4) \times 4 = -8x + 16$.
Le résultat obtenu est $-8x + 16$.
4. a. L'équation $-8x + 16 = 4$ est équivalente à :
$-8x = 4 - 16 = -12$
donc à
$x = \dfrac{-12}{-8} = \dfrac{6}{4}$$= \dfrac{3}{2} = 1,5$.
4. b. Pour obtenir $4$ avec ce programme, il faut donc choisir $\dfrac{3}{2} = 1,5$ comme nombre de départ.
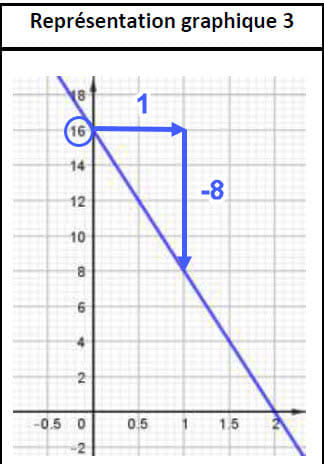
5. La fonction $f$ définie par $f(x) = -8x + 16$ est une fonction affine de coefficient directeur $a = -8$ et d'ordonnée à l'origine $b = 16$.
La seule représentation graphique dont l'ordonnée à l'origine est $16$ et le coefficient directeur est négatif est la n°3.
Exercice 4
Partie A
1. Dans le triangle $\rm{ABC}$ rectangle en $\rm{B}$, d'après le théorème de Pythagore, on a :
$\rm{AC}^2 = \rm{AB}^2 + \rm{BC}^2 = 600^2 + 450^2$$= 360\,000 + 202\,500 = 562\,500$.
On a donc :
$\rm{AC} = \sqrt{562\,500} = 750 ~\rm{m}$.
2. a. Les droites $(\rm{ED})$ et $(\rm{AB})$ sont toutes les deux perpendiculaires à la droite $(\rm{BC})$.
Or, si deux droites sont perpendiculaires à une même droite, alors elles sont parallèles entre elles.
Les droites $(\rm{ED})$ et $(\rm{AB})$ sont donc parallèles.
2. b. On considère les triangles $\rm{ABC}$ et $\rm{EDC}$.
Les points $\rm{C}$, $\rm{E}$ et $\rm{A}$ sont alignés dans cet ordre, et les points $\rm{C}$, $\rm{D}$ et $\rm{B}$ sont aussi alignés dans cet ordre.
D'après la question précédente, les droites $(\rm{ED})$ et $(\rm{AB})$ sont parallèles.
D'après le théorème de Thalès dont les conditions sont vérifiées, on a :
$\dfrac{\rm{CD}}{\rm{CB}} = \dfrac{\rm{DE}}{\rm{AB}}~$$~= \dfrac{\rm{CE}}{\rm{CA}}$ donc en particulier $\dfrac{\rm{CD}}{\rm{CB}} = \dfrac{\rm{DE}}{\rm{AB}}$.
Avec les valeurs numériques : $\dfrac{270}{450} = \dfrac{\rm{DE}}{600}$.
En utilisant l'égalité des produits en croix :
$450 \times \rm{DE} = 270 \times 600= 162\,000$
puis :
$\rm{DE} = \dfrac{162\,000}{450} = 360 ~\rm{m}$.
3. Dans le triangle $\rm{CDE}$ rectangle en $\rm{D}$, le côté $[\rm{DE}]$ est une base et le côté $[\rm{CD}]$ la hauteur associée.
L'aire du triangle $\rm{CDE}$ est donc :
$A_{\rm{CDE}} = \dfrac{\rm{DE} \times \rm{CD}}{2} = \dfrac{360 \times 270}{2}$$= \dfrac{97\,200}{2} = 48\,600 ~\rm{m}^2$.
Partie B
1. Le sac proposé par le vendeur contient un mélange de blé, seigle et pois selon le ratio $16 : 12 : 8$.
L'indication 2 demande un ratio $80 : 60 : 50$, soit en divisant par $5$ chaque valeur, le ratio $16 : 12 : 10$.
La composition du sac du vendeur ne suit donc pas l'indication 2.
2. $\dfrac{48\,600}{10\,000} = 4,86$ donc le mélange de graines doit contenir $4,86 \times 80 = 388,80~ \rm{kg}$ de blé, d'après la répartition du type de graines de l'indication 2.
3. Avec les prix au kilo donnés dans l'indication 1, l'agriculteur va payer :
$388,80 \times 1,40 + 291,60 \times 1,30 + 243 \times 2,10 = 1\,433,70 ~€$.
Avec un budget de $1\,500~ €$, l'agriculteur dispose donc d'un budget suffisant.
Exercice 5
1. Par exemple, Léna peut tester les codes B4 et C9.
2. La probabilité que la grand-mère de Léna ait choisi la lettre C dans son code est $\dfrac{1}{3}$ (1 lettre sur les 3).
3. La probabilité que la grand-mère de Léna ait choisi le chiffre 7 dans son code est $\dfrac{1}{10}$ (1 chiffre sur les 10).
4. Parmi les 10 chiffres, les nombres qui sont premiers sont 2, 3, 5 et 7.
La probabilité que la grand-mère de Léna ait choisi un nombre premier dans son code est $\dfrac{4}{10} = \dfrac{2}{5}$ (4 chiffres sur les 10).
5. a. Pour tester tous les codes, il y a 3 possibilités pour la lettre et 10 pour le chiffre.
Il y a donc $3 \times 10 = 30$ codes possibles.
S'il faut 5 secondes pour tester chaque code, Léna mettra $30 \times 5 = 150 ~\rm{s} = 2 \times 60 ~\rm{s} + 30 ~\rm{s} = 2~ \rm{min} \: 30 ~\rm{s}$ pour les tester tous.
Léna réussira donc à ouvrir la porte de la maison en moins de 3 minutes.
5. b. Si la porte peut être ouverte en moins de 3 minutes, le format de ce code ne garantit pas la sécurité de la maison.
On pourrait améliorer ce système de code en rajoutant une ou des lettres et/ou un ou des chiffres au code actuel : cela augmentera le nombre de codes possibles, donc le temps nécessaire pour tous les tester.
6. a. Si Léna saisit le code B5, le programme affiche « Code faux » pendant 2 secondes.
6. b. D'après ce programme, le code qui permet d'entrer dans l'immeuble de la grand-mère de Léna est B7.