Définition
Un parallélogramme est un quadrilatère dont les côtés opposés sont parallèles.

Propriétés
Propriété 1 : Diagonales
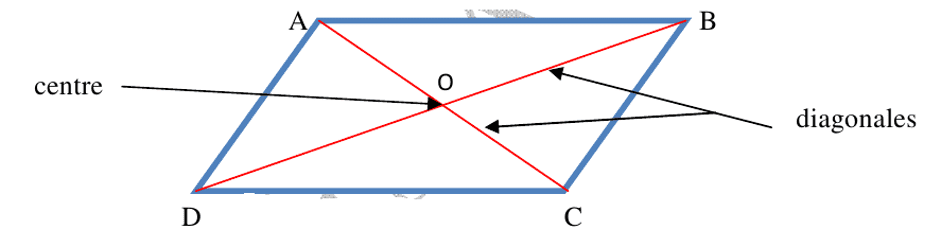
Dans un parallélogramme, les diagonales se coupent en leur milieu. Ce point est le centre de symétrie de ce parallélogramme.
Propriété 2 : Côtés opposés
Dans un parallélogramme, les côtés opposés ont la même mesure.
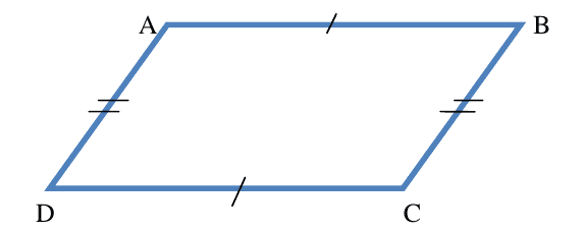
$\rm ABCD$ est un parallélogramme, donc $\rm AB = DC$ et $\rm AD = BC$.
Propriété 3 : Angles
Dans un parallélogramme, deux angles opposés sont égaux. Dans un parallélogramme, deux angles consécutifs sont supplémentaires.

$\mathrm{ABCD}$ est un parallélogramme, donc $\rm\widehat{A}=\rm\widehat{C}$ et $\rm\widehat{B}=\rm\widehat{D}$ :
- $\rm\widehat{A}+\widehat{B}=180^{\circ}$
- $\rm\widehat{B}+\widehat{C}=180^{\circ}$
- $\rm\widehat{C}+\widehat{D}=180^{\circ}$
- $\rm\widehat{D}+\widehat{A}=180^{\circ}$.
Reconnaissances d'un parallélogramme
Critère 1 : Côtés opposés parallèles
Si un quadrilatère a ses côtés opposés parallèles, alors c'est un parallélogramme.

$\rm (AB) // (D C)$ et $\rm (A D) / /(B C)$, donc $\rm A B C D$ est un parallélogramme.
Critère 2 : Diagonales qui se coupent en leur milieu
Si un quadrilatère a ses diagonales qui se coupent en leur milieu, alors c'est un parallélogramme.
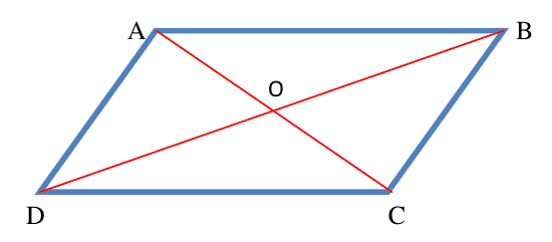
$\rm O$ milieu de $\rm [A C]$ et $\rm O$ milieu de $\rm [BD]$, donc $\rm ABCD$ est un parallélogramme.
Critère 3 : Angles opposés égaux
Si un quadrilatère a ses angles opposés de même mesure, alors c'est un parallélogramme. Si dans un quadrilatère, deux paires d'angles consécutifs quelconques sont supplémentaires, alors c'est un parallélogramme.
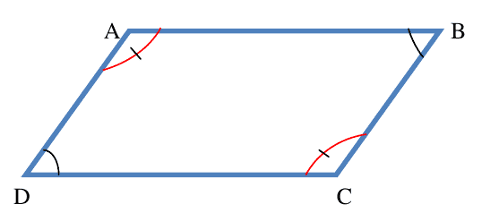
$\rm\widehat{A}=\rm\widehat{C}$ et $\rm\widehat{B}=\rm\widehat{D}$, donc $\mathrm{ABCD}$ est un parallélogramme.
- $\rm\widehat{A}+\widehat{B}=180^{\circ}$
- $\rm \widehat{B}+\widehat{C}=180^{\circ}$
- $\rm \widehat{C}+\widehat{D}=180^{\circ}$
- $\rm \widehat{D} + \widehat{A}=180^{\circ}$.
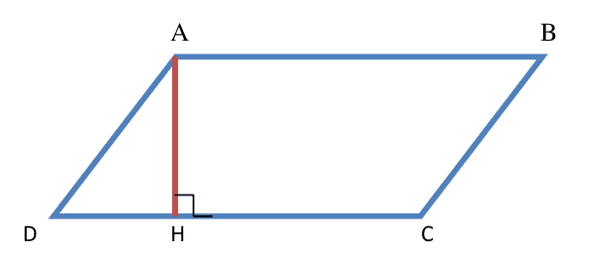
Aire du parallélogramme
Si $\rm ABCD$ est un parallélogramme, alors $\rm \text{Aire} (A B C D)$ $=\text {base} \times \text {hauteur}=$ $\rm D C \times A H$