Ndajaleek angalu bènn ñettoñ
Ci bènn ñettoñ, ndajaleek angal yi mu ngi tollook $180°$.
Su ñu ko waxee neneen, bu $\rm ABC$ nekkee ab ñettoñ, kon da ñuy am $\rm mes \widehat{A} + mes \widehat{B} + mes \widehat{C}=180°$.
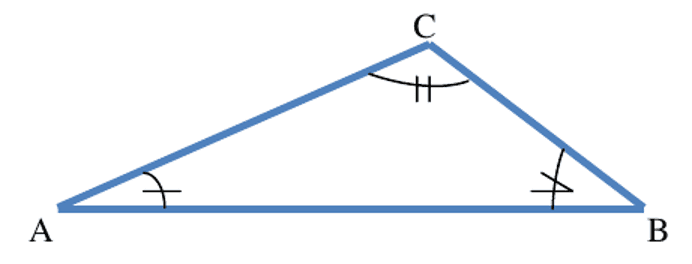
Rëdd yu rañëeku yi
Tasebkawewaay yi
Ci bènn ñettoñ, tasebkawewaay da ñuy dogoo ci bènn tomb. Tomb bòbu mooy nekk diggu mbege miy wërële ñettoñ bi. Maanaam, mbege mòmu da fay jaar ci ñetti puji ñettoñ bi.
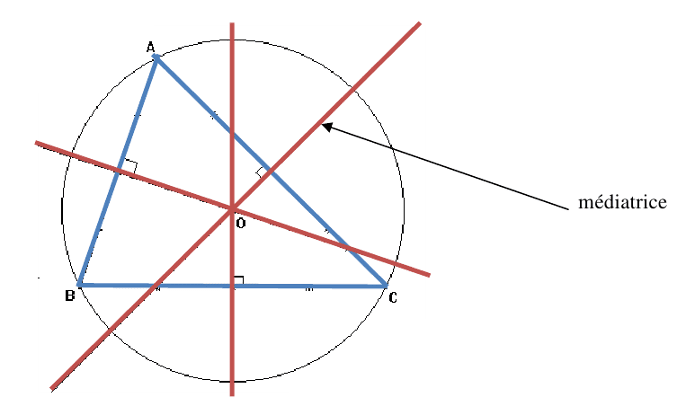
Kawewaay yi
Ci bènn ñettoñ, ñetti kawewaay yi da ñuy dogoo ci bènn tomb. Tomb bòbu mooy jub-diggu (orthocentre) ñettoñ bi.
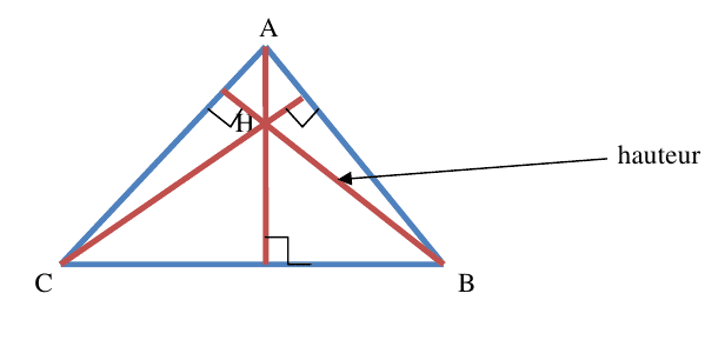
Ñettoñ bu koñjub
Jëfandikukaay yu ñettoñ bu koñjub
- Ci bènn ñettoñ bu koñjub, angal yu xat yi (angles aigus) da ñuy mottaliwante. Maanaam, su fekkee $\mathrm{ABC}$ ab ñettoñ bu koñjub la ci $\mathrm{A}$, kon da ñuy am $\rm\widehat{ABC}+\widehat{ACB}=90°$.
- Ci bènn ñettoñ bu koñjub digguk janokoñjub gi (hypoténuse) da fay nekk digguk mbegeek wërële mi (cercle circonscrit).
- Ci bènn ñettoñ bu koñjub, soreewaayu digguk janokoñjub gi ak pujuk ñettoñ bi ñoo tolloo
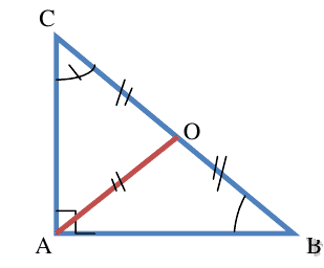
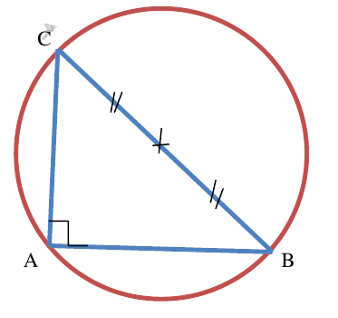
Xammeekaayu bènn ñettoñ bu jub
-
Su ñaari angali bènn ñettoñ mottaliwantee, kon ñettoñ bòbu dafa koñjub. Maanaam, su $\rm ABC$ nekkee bènn ñettoñ te $\rm\widehat{B} + \widehat{C}=90°$, kon $\rm ABC$ da fay nekk koñjub ci $\rm A$.
-
Soo jokkalee bènn tomb bu bènn mbege ak cetiy bènn si jaar-diggam yi bu tomb bòbu bokkul, kon da ngay am bènn ñettoñ bu koñjub. Maanaam, su $\rm ABC$ nekkee bènn ñettoñ bu jub, $\rm A \in(C)$ te $\rm [BC]$ nekk bènn jaar-diggu $\rm (C)$, kon $\rm ABC$ da fay nekk koñjub ci $\rm A$.
-
Su fekkee ne, si bènn ñettoñ, digguk bènn wet dafa tolloo soreewaay ak puj yi, kon ñettoñ bòbu da fa koñjub. Maanaam, su $\rm ABC$ nekkee bènn ñettoñ te $\rm I$ di diggu $\rm [BC]$ te itam $\rm IA=IB=IC$, kon $\rm ABC$ da fa koñjub ci $\rm A$.
Ñettoñ bu ñaariwet-yem
Jëfandikukaay yu ñettoñ bu ñaariwet-yem
Ab ñettoñ bu ñaariwet-yem da fay am aksu safaanoo jàkkaarle
Ci bènn ñettoñ bu wet-yem, ñaari angal yi feetee ci sukkëndikukaay bi ñoo tolloo.
$\rm ABC$ dafa ñaariwet-yem ci $\rm A$, kon $\rm\widehat{B}=\widehat{C}$.
Aksu safaanoo jàkkaarle bi da fay boole nekk :
- taseebkawewaayu sukkëndikukaay bi,
- seddalekañ bu pujum cosaan wi,
- kawewaay ak jaar-diggu sukkëndikukaay bi.
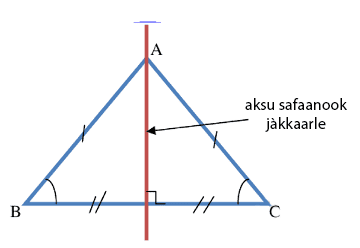
Xammeekaayu bènn ñettoñ bu ñaariwet-yem
- Su bènn ñettoñ amee aksu safaanoo jàkkaarle, kon dafa ñaariwet-yem. Maanaam, su $\rm ABC$ nekkee bènn ñettoñ te $(\Delta)$ bènn aksu safaanook jàkkaarle bu $\rm ABC,$ kon $\rm ABC$ da fay ñaariwet-yem.
- Su bènn ñettoñ amee ñaari angal yu yem natt, kon da fa ñaariwet-yem. Maanaam, su $\rm ABC$ nekkee bènn ñettoñ te su fekkee ne $\rm\widehat{B}=\widehat{C}$, kon $\rm ABC$ da fay ñaariwet-yem ci $\rm A$.
Ñettoñ bu wet-yem
Jëfandikukaay yu ñettoñ bu wet-yem
Ab ñettoñ bu wett-yem da fay am ñetti aksu safaanook jàkkaarle yuy doon taseebkawewaayu wetam yi.
Su bènn ñettoñ wett-yemee, ñetti angallam yi da ñuy yem natt $(60°$ bu ci nekk). Maanaam, su $\rm ABC$ nekkee bènn ñettoñ bu wett-yem, kon $\rm\widehat{A}=\widehat{B}=\widehat{C}=60°$.
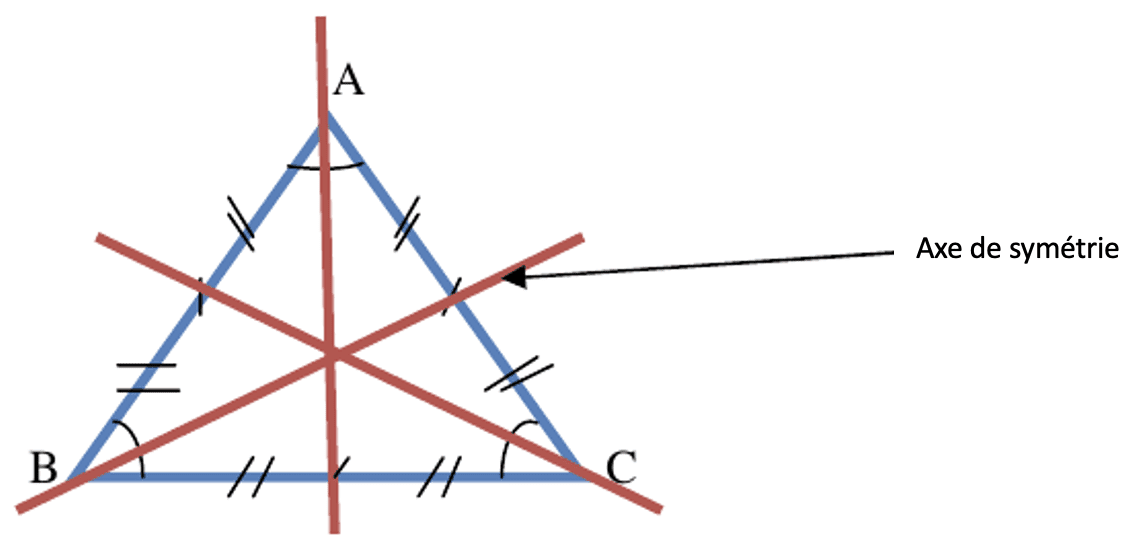
Tombu doganteek ñetti aksu safaanook jàkkaarle yi da fay boole nekk :
- diggu mbegeek wërële mi,
- jub-digg mi.
Xammeekaayu bènn ñettoñ bu wet-yem
-
Su bènn ñettoñ amee ñaari aksu safaanoo jàkkaarle, kon dafa wett-yem. Maanaam, su $(\Delta)$ ak $\left(\Delta^{\prime}\right)$ nekkee ay aksu safaanook jàkkaarle bu ñettoñ bii di $\rm ABC$, kon $\rm ABC$ dafa wett-yem.
-
Su ñetti angalu bènn ñettoñ toolloowee, dafa wett-yem. Maanaam, su $\rm ABC$ nekkee ab ñettoñ te su ñu amee $\rm\widehat{A}=\widehat{B}=\widehat{C}$, kon dafa wett-yem.


