I. Trapèze
Définitions
Un trapèze est un quadrilatère qui a deux côtés de supports parallèles. Les deux autres côtés sont sécants.

Un trapèze rectangle est un trapèze qui un angle droit.

Un trapèze isocèle est un trapèze qui a ses deux côtés de supports sécants de même longueur.
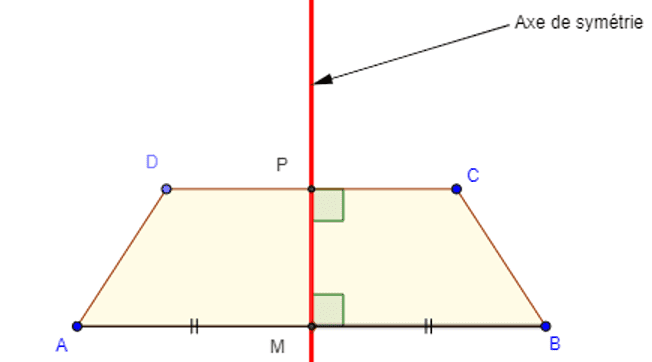
Un trapèze isocèle a un axe de symétrie qui est la médiatrice de ses bases. Un trapèze isocèle a deux angles à la base de même mesure.
Reconnaissances d'un trapèze
- Si un trapèze a angle droit, alors il est rectangle.
- Si un trapèze a deux angles à la base de même mesure, alors il est isocèle.
- Si un trapèze a un axe de symétrie qui est la médiatrice des ses bases, alors il est isocèle.
Aire du trapèze
L'aire du trapèze est égale à la somme de ses bases (grande base + petite base) multipliée par sa hauteur, divisée par $2$.
Autrement dit, $\text{Aire} = \dfrac{(\mathrm B + b)\times h}{2}$ (avec $\rm B$ la grande base, $b$ la petite base et $h$ la hauteur).
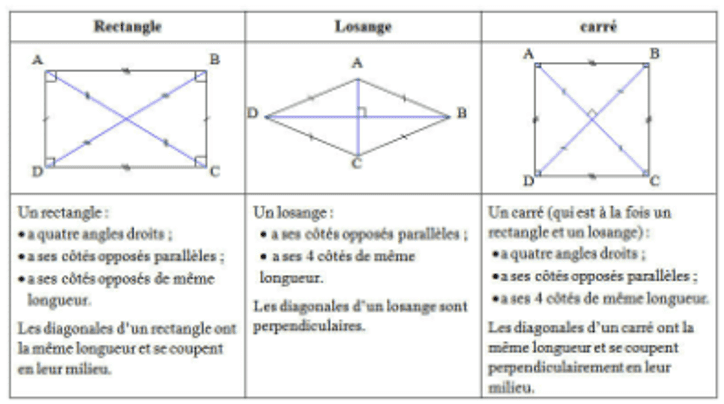
II. Rectangle
Définition
Un rectangle est un quadrilatère qui a quatre angles droits.
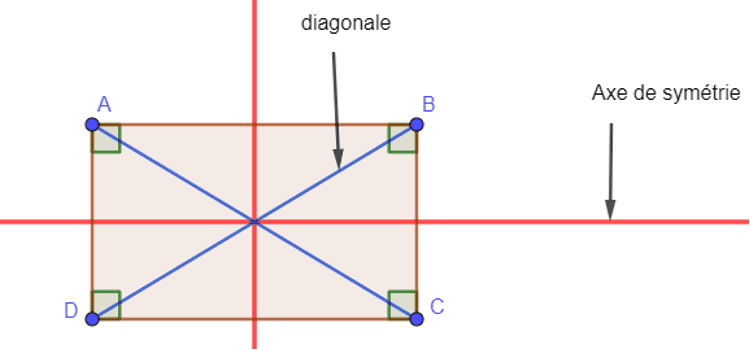
Propriétés
- Les diagonales d'un rectangle ont la même longueur.
- Les médiatrices des côtés d'un rectangle sont des axes de symétrie.
- Dans un rectangle, les diagonales et les axes de symétrie se coupent en son centre de symétrie.
Reconnaissances d'un rectangle
- Si un parallélogramme a un angle droit, alors c'est un rectangle.
- Si un parallélogramme a ses diagonales de même longueur, alors c'est un rectangle.
Aire d'un rectangle
L'aire d'un rectangle est égale au produit de sa longueur par sa largeur.
Autrement dit, Aire = Longueur × largeur.
III. Losange
Définition
Un losange est quadrilatère dont les quatre côtés sont égaux.

Propriétés
- Dans un losange les diagonales se coupent en leur milieu et sont perpendiculaires.
- Un losange admet pour centre de symétrie le point d'intersection de ses diagonales.
- Les diagonales d'un losange sont ses axes de symétrie.
Reconnaissances d'un losange
- Si un parallélogramme a deux côtés consécutifs de même longueur, alors il est un losange.
- Si un parallélogramme a ses diagonales perpendiculaires, alors il est un losange.
- Si un parallélogramme a une diagonale qui est en même temps bissectrice d'un angle, alors il est un losange.
Aire du losange
L'aire d'un losange est égale au produit de ses diagonales divisé par $2$.
IV. Carré
Définition
Un carré est un quadrilatère qui a $4$ côtés de même longueur et $4$ angles droits. Un carré est à la fois un rectangle et un losange.

Propriétés
- Les diagonales d'un carré sont perpendiculaires et de même longueur.
- Un carré a quatre axes de symétrie et un centre de symétrie.
- Un carré a toutes les propriétés du rectangle et du losange.
Reconnaissances d'un carré
- Un carré est un losange particulier :
- Si un losange a un angle droit, alors c'est un carré.
- Si un losange a ses diagonales de même longueur, alors c'est un carré.
- Un carré est un rectangle particulier :
- Si un rectangle a deux côtés consécutifs de même longueur alors c'est un carré.
- Si un rectangle a ses diagonales perpendiculaires, alors c'est un carré.
- Si un quadrilatère est à la fois un losange et un rectangle, alors c'est un carré.
Aire d'un carré
L'aire d'un carré est égale au produit de deux côtés.