Tekki
Takkandeer bu jub bu bènn tomb $\mathrm{M}$ ci bènn rëdd $(d)$ mooy tomb $\mathrm{H}$ biy nekk doganteek rëdd wii di $(d)$ ak jub-dogoo wu $(d)$ miy jaar ci $\rm M$.
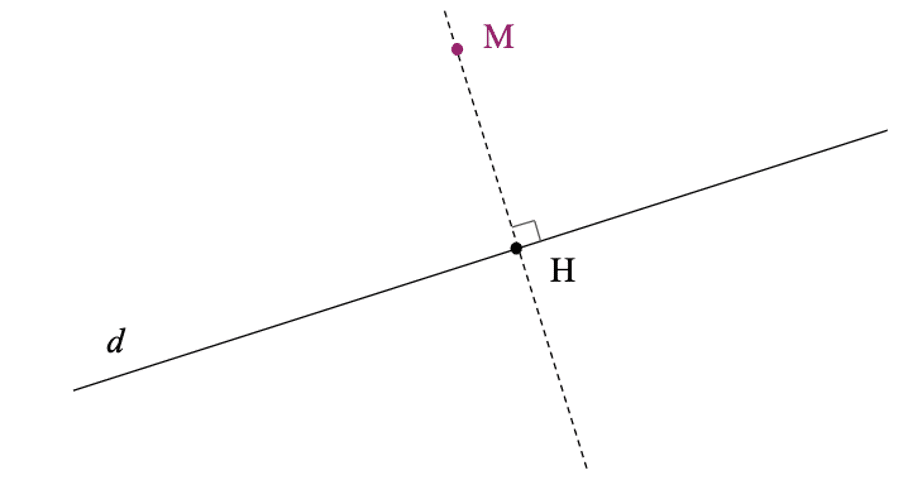
$\rm H$ mooy takkandeer bu jub bu tomb bii di $\mathrm{M}$ ci rëdd wii di $(d)$.
Ay jagle
- Takkandeer bu jub bu bènn dogit ab dogit lay doon woo xamne yènn saayi man na yemook bènn tomb.
- Digguk bènn dogit mu ngi takkandeeree ci diggi dogit biy nataalam.
Xammeeku ci maasale gi
Xàmmikaayu digguk bènn dogit
Su ñu amee $\mathrm{A}\left(x_{\mathrm{A}} ~; y_{\mathrm{A}}\right) ; \mathrm{B}\left(x_{\mathrm{B}} ~; y_{\mathrm{B}}\right)$ ak $\mathrm{M}\left(x_{\mathrm{M}} ~; y_{\mathrm{M}}\right)$. Te su $\rm M$ nekkee digguk dogit wii dit $\rm [AB]$ kon :
$$x_{\mathrm{M}}=\dfrac{x_{\mathrm{A}}+x_{\mathrm{B}}}{2} \text{ ak } y_{\mathrm{M}}=\dfrac{y_{\mathrm{A}}+y_{\mathrm{B}}}{2}$$
Kaare wuk soreewaay ci digante 2 points
Su ñu amee $\mathrm{A}\left(x_{\mathrm{A}}~ ; y_{\mathrm{A}}\right)$ ak $\mathrm{B}\left(x_{\mathrm{B}} ~; y_{\mathrm{B}}\right)$ kon :
$$\mathrm{AB}^2=\left(x_{\mathrm{B}}-x_{\mathrm{A}}\right)^2+\left(y_{\mathrm{B}}-y_{\mathrm{A}}\right)^2$$


