Soreewaay

📝 Mini-cours GRATUIT

Je m’inscris pour accéder gratuitement à ce contenu

Soreewaay

I. Tolluwaayu ñaari mbege

Na $\rm C(O~ ; R)$ ak $\rm C'(O' ~; R')$ nekk 2 mbege.

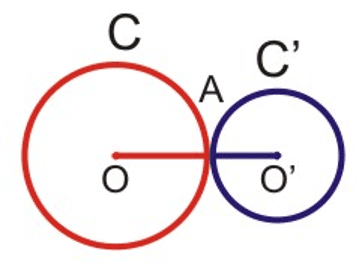
Mbege yu riisoo ci biti

Su soreewaayu 2 digg yi tollook ndajaleek ceeñeer yi, kon mbege yi da ñu riisoo ci biti : $\rm OO' = R + R'$.

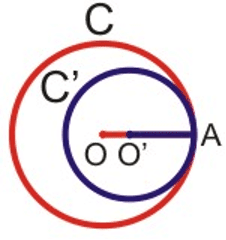
Mbege yu riisoo ci biir

Su soreewaayu digante 2 digg yi tollook waññeekuk ceeñeer yi, kon mbege yi da ñoo riisoo ci biir : $\rm OO'=R - R'$.

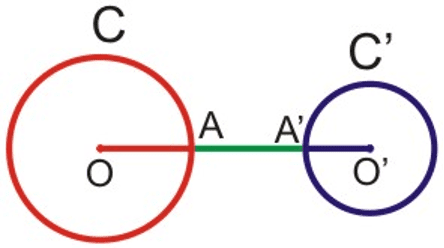
Mbege yu wuute ci biti

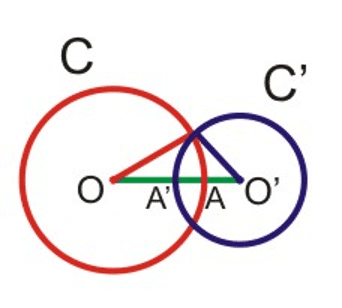
Su soreewaayu digg yi ëppee ndajaleek ceeñeer yi kon ñaari mbege yi da ñoo wuute ci biti : $\rm OO' > R + R'$

Mbege yu wuute ci biir

Su soreewaayu digg yi yèesee waññeekuk ceeñeer yi kon ñaari mbege yi da ñoo wuute ci biir : $\rm OO' \leq R -R'$.

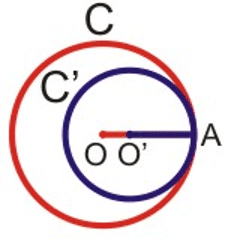
Mbege yu dogoo

Su soreewaayu 2 digg yi nekkee ci digante waññeekuk ceeñeer yi ak seen ndajale, kon ñaari mbege yi da ñoo dogoo : $\rm R-R' \leq OO' \leq R+R'$

II. Soreewaayu bènn tomb ci bènn rëdd

Na $\rm (D)$ nekk bènn rëdd te $\rm M$ di bènn tomb bu nekkul ci $\rm (D)$. Na $\mathrm{H}$ doon tanku jub-dogoob $\rm (D)$ biy jaar ci $\rm M$.

Ngir tomb $\mathrm{A}$ boo jël ci $\rm (D)$, da ñuy am : $\rm MH \leq \mathrm{AM}$. Da ñuy naan $\mathrm{AH}$ mooy soreewaayu tomb bii di $\mathrm{M}$ ci rëdd wii di $\rm (D)$.

III. Jagleek seddale koñ bi

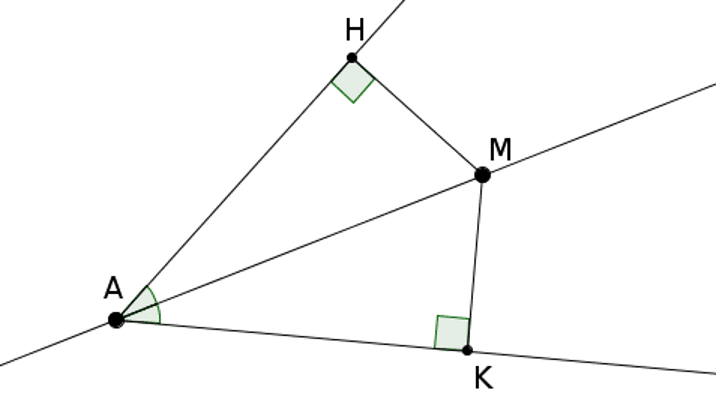
Na $\widehat{\mathrm{HAK}}$ nekk bènn angal te $\rm A$ di ab tomb.

Su $\rm M$ nekkee ci seddaleeb koñu (bissectrice) $\widehat{\mathrm{HAK}}$ ko $\rm M$ da fay yemoo sorewaay ak ñaari weti angal bi.
Su $\rm M$ tolloowee sorewaay ak ñaari weti angal bi, kon da fay nekk ci seddaleeb koñu angal bii di $\widehat{\mathrm{HAK}}$.

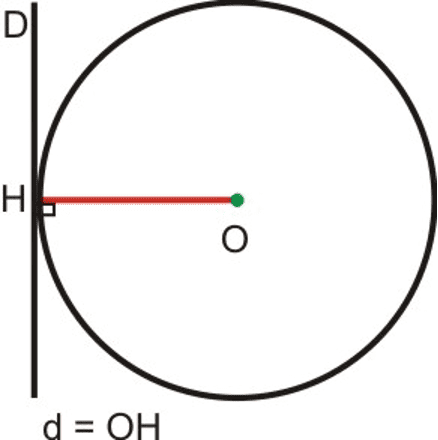
IV. Tolluwaayu bènn rëdd ak bènn mbege

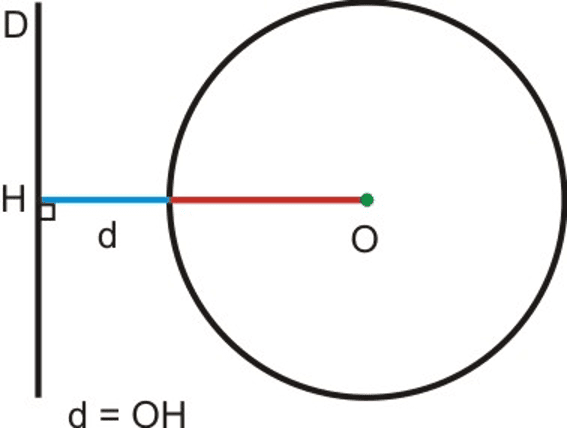
Na $\mathrm{C}(\mathrm{O}, \mathrm{R})$ nekk bènn mbege te $\rm (D)$ di bènn rëdd. Na $\mathrm{OH}=d$ di soreewaayu tomb bii di $\mathrm{O}$ ci rëdd wii di $\rm (D)$.