I. Yokkalanteek ay jëmu

$\rm A$, $\rm B$ et $\rm C$ ñetti tomb la ñuy ci maasale gi. Dèes na tuddee ndajaleek jëmu yii di $\overrightarrow{\rm A B}$ ak $\overrightarrow{\rm B C}$, jëmu jii di $\overrightarrow{\rm A C}$.

Da ñuy binnd : $\overrightarrow{A B}+\overrightarrow{B C}=\overrightarrow{A C}$.

Yemoo gògu ñu ngi koy tuddee yemook Shaal (Chasles).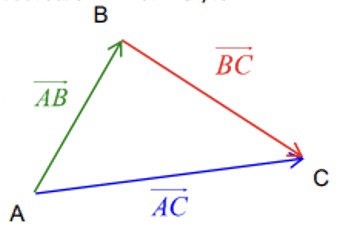

Jëmu yu feewëloo

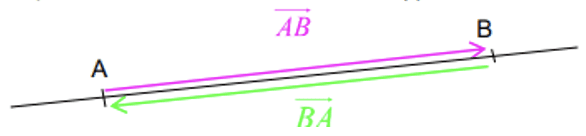
$\rm A$, $\rm B$ ak $\rm C$ ñetti tomb la ñuy ci maasale gi. Da ñuy am : $\rm\overrightarrow{A B}+\overrightarrow{B A}=\overrightarrow{A A}=\overrightarrow{0}$

Da ñuy naan $\rm\overrightarrow{A B}$ ak $\rm\overrightarrow{B A}$ ay jëmu yu feewëloo la ñu. Ñu daal di binnd $\rm\overrightarrow{B A}=-\overrightarrow{A B}$

II. Fŭllanteek bènn jëmu ci bènn limm

Xammee

Dèes na tudddee fŭllanteek jëmu bu dul tus bii di $\rm\overrightarrow{A B}$ ci limum dëgg wii di $k$, jëmu jii di $\rm\overrightarrow{M N}$.

$\rm (A B)~ // ~(M N)$ ñoo bokk jubluwaay
$\rm\overrightarrow{A B}$ ak $\rm\overrightarrow{M N}$ :
- ñoo bokk jëmukaay su fekkee ne $k > 0$
- seeniy jëmukaay yi da ñoo feewëloo su fekkee ne $k < 0$
$\mathrm{M N} = |k| \mathrm{A B}$.

Ab seetlu

Fŭllanteek jëmuk tus gi ci bènn limum dëgg mooy jëmuk tus gi
Fŭllanteek jëmu jii di $\overrightarrow{\rm A B}$ ci $0$ da fay nekk jëmuk tus gi $\overrightarrow{0}$
Fŭllanteek jëmu jii di $\overrightarrow{\rm A B}$ ci bènn limm $k$ bu dul tus dèes na ko binndee : $k \overrightarrow{\rm A B}$.

Ay misaal

Jëmu yii di $\overrightarrow{\rm A B}$, $1.5 \overrightarrow{\rm A B}$ ñoo bokk jubluwaay. $\overrightarrow{\rm A B}$ ak $1,5 \overrightarrow{\rm A B}$ ñoo bokk jëmukaay. $\overrightarrow{\rm A B}$ et $-3 \overrightarrow{\rm A B}$ seeniy jëmukaay yi da ñoo feewëloo.

Ay jagle

$\rm A$, $\rm B$, $\rm C$ ak $\rm D$ ay tomb la ñu ci maasale gi. $k$ ak $h$ ay limum dëgg la ñu. Da ñuy am :

$k(h \overrightarrow{\rm A B})=(k h) \overrightarrow{\rm A B}$.
$k \overrightarrow{\rm A B}+k \overrightarrow{\rm C D}=k(\overrightarrow{\rm A B}+\overrightarrow{\rm C D})$.
$k \overrightarrow{\rm A B}+h \overrightarrow{\rm A B}=(k+h) \overrightarrow{\rm A B}$.
$1 \overrightarrow{\rm A B}=\overrightarrow{\rm A B}$.

III. Jëmu yu bokk jubluwaay ak jëmu yu bokk rëdd (colinéaires)

Jëmu yu bokk jubluwaay

Ab jagle

$\rm A$, $\rm B$, $\rm C$ ak $\rm D$ ñeenti tombi maasale gi la ñu. Wax ne jëmu yii di $\overrightarrow{\rm A B}$ ak $\overrightarrow{\rm C D}$ ñoo bokk jubluwaay mu ngi firi ne mann ngaa gis bènn limm $k$ bu dul tus tey tax ñu am : $\overrightarrow{\rm A B}=k \overrightarrow{\rm C D}$

Jëmu yu bokk rëdd

Xammee

Da ñuy naan ñaari jëmu ñoo bokk rëdd su fekkee ñoo bokk jubluwaay, wala su kènn si ñoom nekkee jëmuk tus gi.

Ab misaal

$\rm \overrightarrow{A B}=3 \overrightarrow{C D}$ mu ngi junj ne $\rm\overrightarrow{A B}$ ak $\rm\overrightarrow{C D}$ ñoo bokk jubluwaay alorste konn $\rm\overrightarrow{A B}$ ak $\rm\overrightarrow{C D}$ ñoo bokk rëdd.

Ab jagle

$\rm A$ ak $\mathrm{B}$ ñaari tomb la ñu si maasale gi. Ne bènn tomb $\rm M$ da fay bokk ci rëdd wii di $(A B)$ mu ngi yemook nga wax ne $\overrightarrow{\rm A M}$ ak $\overrightarrow{\rm A B}$ ñoo bokk rëdd.

Yu tukkee ci lòlu

Jëmu ak digg

Su tomb bii di $\bf I$ doonee digguk $\bf [A B]$, konn $\overrightarrow{\rm A B}=2 \overrightarrow{\rm A I}$

Su fekkee $\overrightarrow{\bf A B}=2 \overrightarrow{\bf A I}$ konn $\rm I$ mooy digguk dogit wii di $\rm [AB]$.

Tomb yu raŋale

Su $\bf A$, $\bf B$ ak $\bf C$ raŋalee konn $\overrightarrow{\rm A C}=k \overrightarrow{\rm A B} \quad k \neq 0$

Su $\overrightarrow{\rm A C}=k \overrightarrow{\rm A B} \quad k \neq 0$ konn $\bf A$, $\bf B$ ak $\bf C$ da ñoo raŋale.

Rëdd yu wetlàŋ

Su $\rm (A B) // (C D)$ konn $\rm \overrightarrow{AB}=k \overrightarrow{\rm CD} \quad k \neq 0$

Su $\rm \overrightarrow{\rm AB}=k \overrightarrow{\rm CD} \quad k \neq 0$ konn $(AB)$ ak $(CD)$ da ñoo wetlàŋ.

I. Yokkalanteek ay jëmu

Jëmu yu feewëloo

II. Fŭllanteek bènn jëmu ci bènn limm

Xammee

Ab seetlu

Ay jagle

III. Jëmu yu bokk jubluwaay ak jëmu yu bokk rëdd (colinéaires)

Jëmu yu bokk jubluwaay

Ab jagle

Jëmu yu bokk rëdd

Xammee

Ab jagle

Yu tukkee ci lòlu

Jëmu ak digg

Tomb yu raŋale

Rëdd yu wetlàŋ

RÉSUMÉ

Jëmu yi

📝 Mini-cours GRATUIT

Jëmu yi

🎲 Quiz GRATUIT

NOMAD EDUCATION

L’app unique pour réussir !

Pour profiter de votre abonnement, rendez-vous dans l’app ou sur le site internet, avec le compte email associé à l’achat