Définition
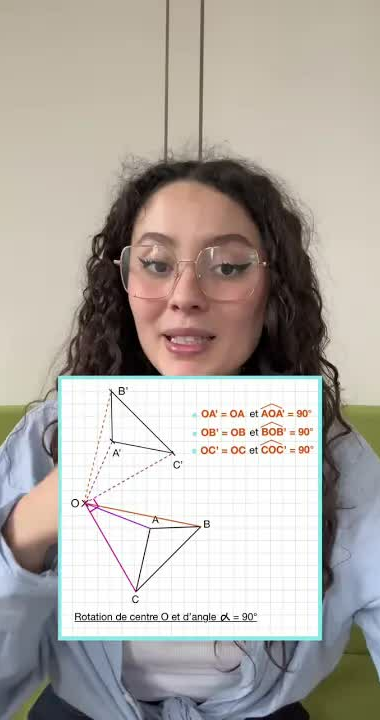
Une rotation est définie par un point $\rm O$ du plan, qui est le centre de la rotation, et un angle de mesure $\alpha^{\circ}$ ($\alpha$ un nombre positif) avec un sens de rotation.
Sens de rotation
Le sens des aiguilles d'une montre est appelé sens indirect et son sens inverse, sens direct.
Image d'un point par rotation
Le point $\rm A'$, qui est l'image d'un point $\rm A$ du plan par cette rotation dont un sens est donné, est tel que :
- $\rm OA' = OA$
- $\rm \widehat{AOA'} = \alpha^{\circ}$.
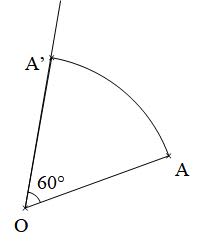
Sur la figure ci-dessous, le point $\rm A'$ est l'image du point $\rm A$ par la rotation de centre $\rm O$ et d'angle $60^{\circ}$ dans le sens inverse des aiguilles d'une montre.
$\rm OA' = OA$ et $\rm \widehat{AOA'} = 60^{\circ}$.
Construction géométrique
Pour le placer, on utilise un compas pour tracer un arc de cercle de centre $\rm O$ et de rayon $\rm OA$ (car $\rm OA' = OA$) et un rapporteur pour tracer la demi-droite $\rm [OA')$ telle que $\rm \widehat{AOA'} = 60^{\circ}$, dans le sens inverse des aiguilles d'une montre. Le point $\rm A'$ est situé à l'intersection de l'arc de cercle et de la demi-droite $\rm [OA')$.
Propriétés
Une rotation :
- conserve les distances : un segment et son image ont la même longueur
- conserve l'alignement : l'image d'une droite est une droite
- conserve les angles : un angle et son image ont la même mesure
- conserve le parallélisme : les images de deux droites parallèles sont deux droites parallèles.