I. Addition vectorielle
$\rm A$, $\rm B$ et $\rm C$ sont trois points du plan. On appelle somme des vecteurs $\overrightarrow{\rm A B}$ et $\overrightarrow{\rm B C}$, le vecteur $\overrightarrow{\rm A C}$.
On note : $\overrightarrow{A B}+\overrightarrow{B C}=\overrightarrow{A C}$.
Cette égalité est appelée égalité de Chasles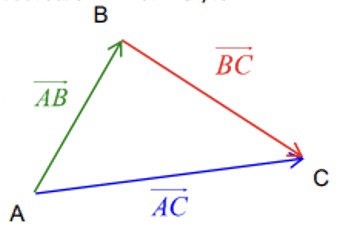
Vecteurs opposés
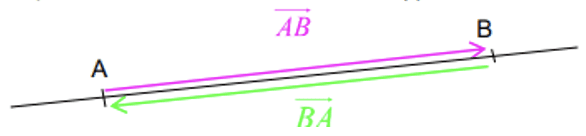
$\rm A$, $\rm B$ et $\rm C$ sont trois points du plan. On a : $\overrightarrow{A B}+\overrightarrow{B A}=\overrightarrow{A A}=\overrightarrow{0}$
On dit que $\rm\overrightarrow{A B}$ et $\overrightarrow{\rm B A}$ sont des vecteurs opposés. On note $\rm\overrightarrow{B A}=-\overrightarrow{A B}$
II. Multiplication d'un vecteur par un nombre
Définition
On appelle produit du vecteur non nul $\rm\overrightarrow{A B}$ par le nombre réel non nul $k$, le vecteur $\rm\overrightarrow{M N}$.
- $\rm (A B)$ et $\rm (M N)$ ont la même direction
- $\rm\overrightarrow{A B}$ et $\rm\overrightarrow{M N}$ :
- ont le même sens si $k > 0$
- ont des sens contraires si $k < 0$
- $\mathrm{M N} = |k| \mathrm{A B}$.
Remarque :
- Le produit du vecteur nul par un nombre réel est le vecteur nul
- Le produit du vecteur $\overrightarrow{\rm A B}$ par $0$ est le vecteur nul $\overrightarrow{0}$
- Le produit du vecteur $\overrightarrow{\rm A B}$ par un nombre $k$ non nul est noté : $k \overrightarrow{\rm A B}$.

Les vecteurs $\overrightarrow{\rm A B}$, $1.5 \overrightarrow{\rm A B}$ ont la même direction. $\overrightarrow{\rm A B}$ et $1,5 \overrightarrow{\rm A B}$ sont de même sens. $\overrightarrow{\rm A B}$ et $-3 \overrightarrow{\rm A B}$ sont de sens contraire.
Propriétés
$\rm A$, $\rm B$, $\rm C$ et $\rm D$ sont des points du plan. $k$ et $h$ sont des nombres réels. On a :
- $k(h \overrightarrow{\rm A B})=(k h) \overrightarrow{\rm A B}$.
- $k \overrightarrow{\rm A B}+k \overrightarrow{\rm C D}=k(\overrightarrow{\rm A B}+\overrightarrow{\rm C D})$.
- $k \overrightarrow{\rm A B}+h \overrightarrow{\rm A B}=(k+h) \overrightarrow{\rm A B}$.
- $1 \overrightarrow{\rm A B}=\overrightarrow{\rm A B}$.
III. Vecteurs de même direction et vecteurs colinéaires
Vecteurs de même direction
Propriété
$\rm A$, $\rm B$, $\rm C$ et $\rm D$ sont quatre points du plan. Les vecteurs $\overrightarrow{\rm A B}$ et $\overrightarrow{\rm C D}$ ont la même direction signifie qu'on peut trouver un nombre réel $k$ non nul tel que : $\overrightarrow{\rm A B}=k \overrightarrow{\rm C D}$
Vecteurs colinéaires
Définition
On dit que des vecteurs sont colinéaires lorsqu'ils ont la même direction, ou lorsque l'un d'eux est le vecteur nul.
Exemple$\rm \overrightarrow{A B}=3 \overrightarrow{C D}$ équivaut à $\rm\overrightarrow{A B}$ et $\rm\overrightarrow{C D}$ ont même direction alors $\rm\overrightarrow{A B}$ et $\rm\overrightarrow{C D}$ sont colinéaires.
Propriété
$\rm A$ et $\mathrm{B}$ sont deux points du plan. Un point $\rm M$ appartient à la droite $(A B)$ équivaut à $\overrightarrow{\rm A M}$ et $\overrightarrow{\rm A B}$ sont colinéaires.
Conséquences
Vecteur et milieu
Si le point $I$ est le milieu de $[A B]$, alors $\overrightarrow{\rm A B}=2 \overrightarrow{\rm A I}$
![]()
Si $\overrightarrow{A B}=k \overrightarrow{A I}$ alors $\rm I$ est le milieu de $\rm [AB]$.
Points alignés
Si $A$, $B$ et $C$ sont alignés alors $\overrightarrow{\rm A C}=k \overrightarrow{\rm A B} \quad k \neq 0$
![]()
Si $\overrightarrow{\rm A C}=k \overrightarrow{\rm A B} \quad k \neq 0$ alors $A$, $B$ et $C$ sont alignés
Droites parallèles
Si $\rm (A B) // (C D)$ alors $\rm \overrightarrow{AB}=k \overrightarrow{\rm CD} \quad k \neq 0$

Si $\rm \overrightarrow{\rm AB}=k \overrightarrow{\rm CD} \quad k \neq 0$ alors $(AB)$ et $(CD)$ sont parallèles.





