Résistance électrique

📝 Mini-cours GRATUIT

Je m’inscris pour accéder gratuitement à ce contenu

Résistance électrique

I. Résistance électrique

Une résistance électrique se présente sous forme de petit cylindre sur lequel sont peints des anneaux de couleurs. Elle permet de modifier l’intensité du courant dans un circuit électrique. Elle peut être branchée indifféremment dans un sens ou dans l’autre.

NB : le rhéostat est une résistance réglable. Elle permet de modifier progressivement l’intensité du courant électrique dans le circuit

Symbole de la résistance électrique :

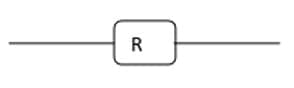
Symbole du rhéostat :

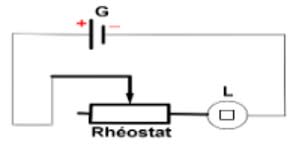
II. Étude expérimentale d’un résistor

1. Expérience

Lorsqu’on déplace le curseur, l’intensité $I$ du courant qui traverse la résistance varie, la tension $U$ varie dans le même sens. Les résultats de mesures sont consignés dans le tableau ci-contre :

La représentation graphique : $U=f(I)$ est appelée caractéristique de la résistance.

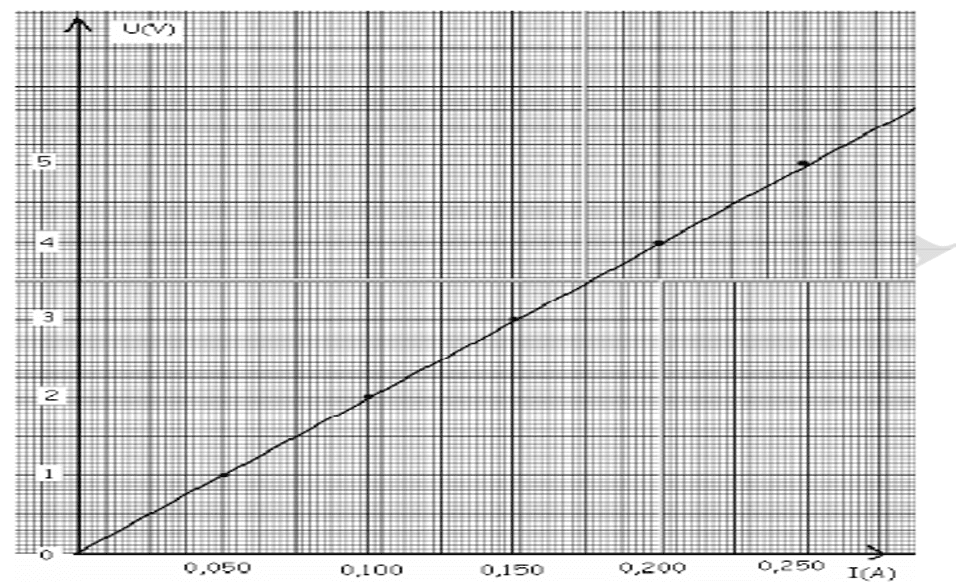
2. Loi d’Ohm

La caractéristique étant une droite qui passe par l’origine, $U$ et $I$ sont proportionnelles et $R$ est la constante de proportionnalité.

Énoncé de la loi d’Ohm

La tension électrique entre deux points d’un résistor est égale au produit de sa résistance par l’intensité $I$ du courant électrique qui le traverse :

$\color{orangered}{U=R \times I}$

avec

$\color{orangered}{\left\{\begin{array}\\U: \text { tension en volt (V)} \\ I: \text { intensité du courant en ampère (A)} \\ R: \text { résistance en ohm }(\Omega)\end{array}\right.}$

NB : la tension se mesure avec un voltmètre et se branche toujours en parallèle avec le dipôle dont on veut mesurer la tension.

3. Détermination de la résistance d’un conducteur ohmique à partir de la caractéristique

$\color{orangered}{R=\dfrac{\Delta U}{\Delta I}=\dfrac{U_f-U_i}{I_f-I_i}}$

Exemple :

$\color{orangered}{R=\dfrac{\Delta U}{\Delta I}=\dfrac{2-1}{1-0,05}=20 ~\Omega}$

Remarque : la résistance électrique se mesure par un ohmmètre.

III. Résistance d’un fil cylindrique homogène de section constante

La résistance d’un fil cylindrique homogène de section constante est donnée par la relation :

$\color{orangered}{R=\rho \times \dfrac{l}{s}}$

avec

$\left\{\begin{array} \
{l} \text { : longueur du fil en mètre (m) } \\ \rho : \text { résistivité du matériau en } \Omega \cdot \rm m \\ s\text { : section droite du fil en } \mathrm {m^2}\end{array}\right.$

$\color{orangered}{s=\pi \times r^2}$ où $r$ est le rayon de la section du fil.