I. Yokkalanteek ay jëmu
$\rm A$, $\rm B$ et $\rm C$ ñetti tomb la ñuy ci maasale gi. Dèes na tuddee ndajaleek jëmu yii di $\overrightarrow{\rm A B}$ ak $\overrightarrow{\rm B C}$, jëmu jii di $\overrightarrow{\rm A C}$.
Da ñuy binnd : $\overrightarrow{A B}+\overrightarrow{B C}=\overrightarrow{A C}$.
Yemoo gògu ñu ngi koy tuddee yemook Shaal (Chasles).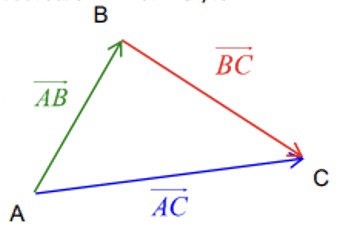
Jëmu yu feewëloo
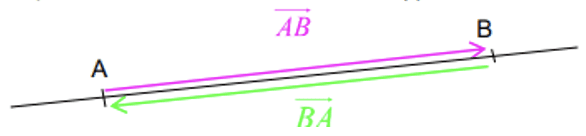
$\rm A$, $\rm B$ ak $\rm C$ ñetti tomb la ñuy ci maasale gi. Da ñuy am : $\rm\overrightarrow{A B}+\overrightarrow{B A}=\overrightarrow{A A}=\overrightarrow{0}$
Da ñuy naan $\rm\overrightarrow{A B}$ ak $\rm\overrightarrow{B A}$ ay jëmu yu feewëloo la ñu. Ñu daal di binnd $\rm\overrightarrow{B A}=-\overrightarrow{A B}$
II. Fŭllanteek bènn jëmu ci bènn limm
Xammee
Dèes na tudddee fŭllanteek jëmu bu dul tus bii di $\rm\overrightarrow{A B}$ ci limum dëgg wii di $k$, jëmu jii di $\rm\overrightarrow{M N}$.
- $\rm (A B)~ // ~(M N)$ ñoo bokk jubluwaay
- $\rm\overrightarrow{A B}$ ak $\rm\overrightarrow{M N}$ :
- ñoo bokk jëmukaay su fekkee ne $k > 0$
- seeniy jëmukaay yi da ñoo feewëloo su fekkee ne $k < 0$
- $\mathrm{M N} = |k| \mathrm{A B}$.
Ab seetlu
- Fŭllanteek jëmuk tus gi ci bènn limum dëgg mooy jëmuk tus gi
- Fŭllanteek jëmu jii di $\overrightarrow{\rm A B}$ ci $0$ da fay nekk jëmuk tus gi $\overrightarrow{0}$
- Fŭllanteek jëmu jii di $\overrightarrow{\rm A B}$ ci bènn limm $k$ bu dul tus dèes na ko binndee : $k \overrightarrow{\rm A B}$.

Jëmu yii di $\overrightarrow{\rm A B}$, $1.5 \overrightarrow{\rm A B}$ ñoo bokk jubluwaay. $\overrightarrow{\rm A B}$ ak $1,5 \overrightarrow{\rm A B}$ ñoo bokk jëmukaay. $\overrightarrow{\rm A B}$ et $-3 \overrightarrow{\rm A B}$ seeniy jëmukaay yi da ñoo feewëloo.
Ay jagle
$\rm A$, $\rm B$, $\rm C$ ak $\rm D$ ay tomb la ñu ci maasale gi. $k$ ak $h$ ay limum dëgg la ñu. Da ñuy am :
- $k(h \overrightarrow{\rm A B})=(k h) \overrightarrow{\rm A B}$.
- $k \overrightarrow{\rm A B}+k \overrightarrow{\rm C D}=k(\overrightarrow{\rm A B}+\overrightarrow{\rm C D})$.
- $k \overrightarrow{\rm A B}+h \overrightarrow{\rm A B}=(k+h) \overrightarrow{\rm A B}$.
- $1 \overrightarrow{\rm A B}=\overrightarrow{\rm A B}$.
III. Jëmu yu bokk jubluwaay ak jëmu yu bokk rëdd (colinéaires)
Jëmu yu bokk jubluwaay
Ab jagle
$\rm A$, $\rm B$, $\rm C$ ak $\rm D$ ñeenti tombi maasale gi la ñu. Wax ne jëmu yii di $\overrightarrow{\rm A B}$ ak $\overrightarrow{\rm C D}$ ñoo bokk jubluwaay mu ngi firi ne mann ngaa gis bènn limm $k$ bu dul tus tey tax ñu am : $\overrightarrow{\rm A B}=k \overrightarrow{\rm C D}$
Jëmu yu bokk rëdd
Xammee
Da ñuy naan ñaari jëmu ñoo bokk rëdd su fekkee ñoo bokk jubluwaay, wala su kènn si ñoom nekkee jëmuk tus gi.
Ab misaal$\rm \overrightarrow{A B}=3 \overrightarrow{C D}$ mu ngi junj ne $\rm\overrightarrow{A B}$ ak $\rm\overrightarrow{C D}$ ñoo bokk jubluwaay alorste konn $\rm\overrightarrow{A B}$ ak $\rm\overrightarrow{C D}$ ñoo bokk rëdd.
Ab jagle
$\rm A$ ak $\mathrm{B}$ ñaari tomb la ñu si maasale gi. Ne bènn tomb $\rm M$ da fay bokk ci rëdd wii di $(A B)$ mu ngi yemook nga wax ne $\overrightarrow{\rm A M}$ ak $\overrightarrow{\rm A B}$ ñoo bokk rëdd.
Yu tukkee ci lòlu
Jëmu ak digg
Su tomb bii di $\bf I$ doonee digguk $\bf [A B]$, konn $\overrightarrow{\rm A B}=2 \overrightarrow{\rm A I}$
![]()
Su fekkee $\overrightarrow{\bf A B}=2 \overrightarrow{\bf A I}$ konn $\rm I$ mooy digguk dogit wii di $\rm [AB]$.
Tomb yu raŋale
Su $\bf A$, $\bf B$ ak $\bf C$ raŋalee konn $\overrightarrow{\rm A C}=k \overrightarrow{\rm A B} \quad k \neq 0$
![]()
Su $\overrightarrow{\rm A C}=k \overrightarrow{\rm A B} \quad k \neq 0$ konn $\bf A$, $\bf B$ ak $\bf C$ da ñoo raŋale.
Rëdd yu wetlàŋ
Su $\rm (A B) // (C D)$ konn $\rm \overrightarrow{AB}=k \overrightarrow{\rm CD} \quad k \neq 0$

Su $\rm \overrightarrow{\rm AB}=k \overrightarrow{\rm CD} \quad k \neq 0$ konn $(AB)$ ak $(CD)$ da ñoo wetlàŋ.


