Équations et systèmes d’équations à 2 inconnues

I. Équations à 2 inconnues

Une équation à 2 inconnues est de la forme $ax+by+c=0$ $(a$ ; $b$ et $c$ sont des réels$)$.

Recherche des solutions d'une équation du 1^er degré dans $\mathbb{R} \times \mathbb{R}$

Méthode :

Pour trouver un couple de réels solution d'une équation du 1^er degré dans $\mathbb{R} \times \mathbb{R}$, on attribue une valeur arbitraire à l'une des inconnues et on détermine l'autre.

Dans $\rm(E_1)$ : $y=-2x+6$, si $x=0$ alors $y=-2 \times 0+6$ donc $y=6$

Le couple de points $(0 ; 6)$ est une solution de $\rm(E_1)$. Si $x=2$, alors $y = -2 \times 2 +6$ donc $y = 2$.

Le couple de réels $(2 ; 2)$ est une solution de $\rm(E_1)$.

Représentation graphique des solutions d'une équation dans $\mathbb{R} \times \mathbb{R}$

On sait que les couples de réels $(0 ; 6)$ ; $(1 ; 4)$ et $(2 ; 2)$ sont solutions de l'équation $(\mathrm E) : 2x+y=6$.

Dans le plan muni d'un repère $\rm (O, I, J)$ plaçons les points $\rm A(0 ; 6)$ ; $\rm B(1 ; 4)$ et $\rm C(2 ; 2)$.

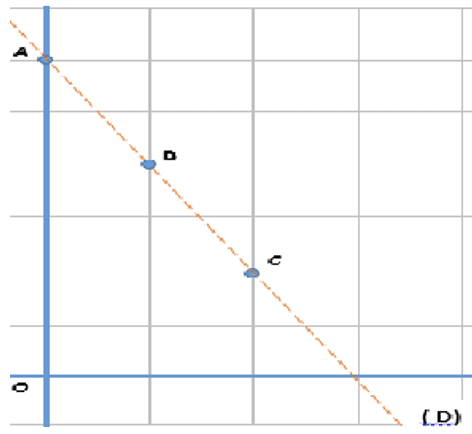
On remarque que les points $\rm A(0 ; 6)$ ; $\rm B(1 ; 4)$ et $\rm C(2 ; 2)$ sont alignés.

Si une droite $\rm (D)$ passe par les points $\rm A, B$ et $\rm C$, on dit que la droite $\rm (D)$ d'équation $(\mathrm E): 2x+y=6$ est une équation de la droite $\rm (D)$.

II. Systèmes d'équations à 2 inconnues

Il s'agit des systèmes du type :

$$\left\{\begin{array}{l} ax+by=c \\ a'x+b'y=c' \end{array}\right.$$

$a$, $b$, $c$, $a'$, $b'$ et $c'$ sont des réels. $x$ et $y$ sont les inconnues. Pour résoudre un tel système, 4 méthodes sont possibles :

Méthode de substitution

Soit le système :

$$\left\{\begin{array}{l} 3x-4y-5=0 \\ 2x+5y-11=0 \end{array}\right.$$

Dans $\rm (D)$ : $3x-4y-5=0$ exprimons $y$ en fonction de $x$ :

$\rm (D_1)$ : $y=\dfrac{3}{4}x-\dfrac{5}{4}$

Dans $\rm(D')$ : $2x+5y-11=0$, remplaçons $y$ par son expression :

$$\begin{array}{l} 2x+5\left(\dfrac{3}{4}x-\dfrac{5}{4}\right)-11=0 \\ x=3 \end{array}$$

Déterminons la valeur de $y$ :

$$\begin{array}{l} y=\dfrac{3}{4}x-\dfrac{5}{4}=\dfrac{3}{4} \times 3-\dfrac{5}{4} \\ y=1 \end{array}$$

On vérifie que le couple $(3 ; 1)$ est solution de $\rm (D)$ et $\rm (D')$ alors la solution du système est le couple $(3 ; 1)$.

La méthode de substitution consiste à exprimer l'une des inconnues en fonction de l'autre dans l'une des deux équations et de la remplacer dans l'autre afin d'obtenir une équation du 1^er degré à une inconnue.

Méthode de combinaison ou d'addition

Soit le système :

$$\left\{\begin{array}{l} 3x-4y-5=0 \\ 2x+5y-11=0 \end{array}\right.$$

✓ Élimination de $x$ :

$$\left\{\begin{array}{l} (3x-4y-5=0) \times (2)\\ (2x+5y-11=0) \times (-3) \end{array}\right.$$

On obtient :

$$\left\{\begin{array}{l} 6x-8y-10=0 \\ -6x-15y+33=0 \end{array}\right.$$

En additionnant membre à membre, on obtient :

$0-23y+23=0$

$23y=23$

$y=1$

✓ Élimination de $y$ :

$$\left\{\begin{array}{l} (3x-4y-5=0) \times (5)\\ (2x+5y-11=0) \times (4) \end{array}\right.$$

On obtient :

$$\left\{\begin{array}{l} 15x-20y-25=0 \\ 8x+20y-44=0 \end{array}\right.$$

En additionnant membre à membre, on obtient :

$23x+0-69=0$

$23x=69$

$x=3$

On vérifie que le couple $(3 ; 1)$ est solution de $\rm (D)$ et $\rm (D')$ alors le couple $(3 ; 1)$ est la solution du système.

Pour résoudre un système par combinaison :

1. On choisit l'inconnue que l'on veut éliminer, par exemple $x$.
2. On multiplie les deux membres de l'une des équations (ou les deux équations, si nécessaire) par des coefficients de sorte que la variable $x$ ait des coefficients opposés.
3. On additionne membre à membre les deux nouvelles équations obtenues en 2. et on obtient une nouvelle équation du premier degré à une inconnue $y$.
4. On résout l'équation en 3., et on trouve la valeur de $y$.
5. On élimine la deuxième inconnue en suivant les étapes énoncées précédemment.
6. On donne la solution du système.

Méthode graphique

Pour résoudre graphiquement le système : $\left\{\begin{array}{l}x+2y=3 \\ 2x-y=1\end{array}\right.$, on trace les droites $\rm (D)$ et $\rm (D')$ d'équations respectives $x+2y=3$ et $2x-y=1$.

$\rm (D)$ et $\rm (D')$ se coupent au point $\rm A$ de coordonnées $(1 ; 1)$.

Donc le couple $(1 ; 1)$ est la solution du système.

Méthode de comparaison

On écrit les deux équations sous forme fonctionnelle :

$2x+3y=4$ donne $y=\dfrac{-2}{3}x + \dfrac{4}{3}$

$5x+6y=7$ donne $y=\dfrac{-5}{6}x+\dfrac{7}{6}$

On compare :

$$\begin{array}{l} -\dfrac{2}{3}x+\dfrac{4}{3}=-\dfrac{5}{6}x+\dfrac{7}{6} \\ \dfrac{5}{6}x-\dfrac{2}{3}x=\dfrac{7}{6}-\dfrac{4}{3} \\ \dfrac{1}{6}x=-\dfrac{1}{6} \\ x=-1 \end{array}$$

En remplaçant dans l'une ou l'autre des équations du système, on trouve la valeur de $y$ :

$$\begin{array}{l} y=-\dfrac{2}{3}(-1)+\dfrac{4}{3}=\dfrac{2}{3}+\dfrac{4}{3}=2 \\ y=2 \end{array}$$

Le couple solution est $x=-1$, $y=2$