I. Application affine
Définition
Soit $a$ et $b$ deux nombres fixés. On appelle application affine de coefficient $a$ et de terme constant $b$, la correspondance $f$ qui à chaque nombre réel $x$ associe le nombre réel $ax+b$.
On note : $f: x \mapsto ax+b$. $ax+b$ est l'image de $x$ par $f$ et on note $f(x)=ax+b$. Si $f(x)=y$ on dit que : $y$ est l'image de $x$ par $f$.
Dans l'écriture $ax+b$, $a$ s'appelle le coefficient ; $b$ s'appelle le terme constant.
ExempleLa correspondance $f$ : $x \mapsto 2x+1$ est une application affine.
- $2$ est le coefficient et $1$ est le terme constant.
Cas particuliers
- Si $a=0$ alors $f(x) = b$. L'application $f$ est constante.
- Si $b=0$ alors $f(x) = ax$. L'application $f$ est linéaire.
Représentation graphique
La représentation graphique de l'application affine $f : \mathbb{R} \rightarrow \mathbb{R}$ $x \rightarrow f(x)=ax+b$ est une droite passant par $M(0;b)$ et de coefficient directeur $a$.
Variation
L'application affine $f: \mathbb{R} \rightarrow \mathbb{R}$ $x \rightarrow f(x)=ax+b$ est :
- croissante si $a > 0$
- décroissante si $a<0$
- constante si $a=0$
Détermination d'une application affine
ExempleSoit $f$ une application affine telle que : $f(2)=-3$ et $f(4)=1$. Détermine l'expression de $f(x)$ pour tout nombre réel $x$.
Cela revient à déterminer les nombres réels $a$ et $b$ tels que $f(x)=ax+b$. On sait que :
$f(2)=-3$. Donc : $2a+b=-3$
$f(4)=1$. Donc : $4a+b=1$
On obtient le système de deux équations à deux inconnues suivant :
$$\left\{\begin{array}{ll} 2a+b=-3&(1) \\ 4a+b=1&(2) \end{array}\right.$$
Nous allons résoudre ce système par substitution. L'égalité $(1)$ : $2a+b=-3$ équivaut à $b=-2a-3 \quad (3)$
Ainsi en remplaçant $b$ par $(-2a-3)$ dans l'égalité $(2)$ on a :
$4a+(-2a-3)=1$
équivaut à $2a-3=1$
équivaut à $2a=4$
équivaut à $a=2$
On a donc $a=2$. On obtient $b$ en remplaçant $a$ par sa valeur dans l'égalité $(3)$ :
$b=-2a-3$
$b=-2 \times 2-3$
$b=-7$
Donc : $f(x)=2x-7$.
II. Application affine par intervalles
Soit $f$ une application définie par $f(x)=|-3x+6|$
Montrons que $f$ est une application affine par intervalle
On a $-3x+6=0$ si, et seulement si, $x=2$
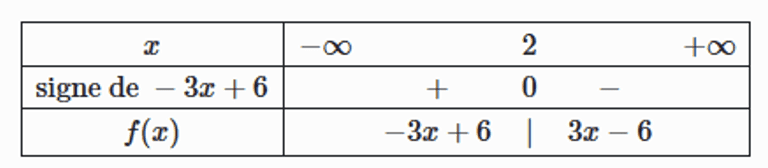
Si $x \leq 2$, alors $f(x)=-3x+6$
Si $x \geq 2$, alors $f(x)=3x-6$
D'où, $f$ est une application affine par intervalle.
Représentation graphique
Représentons graphiquement $f(x)=|-3x+6|$
Représenter graphiquement $f$ c'est représenter :
$(D_1) : y=-3x+6$ pour $x \leq 2$ et $(D_2) : y=3x-6$ pour $x \geq 2$
Ainsi, on a :
Si $x=1$, alors $y = 3$, on obtient le point A et si $x=2$, alors $y=0$, on obtient le point B.
Si $x = 3$, alors $y = 3$, on obtient le point C.
Ainsi, on obtient la courbe suivante :






