Trigonométrie 3ème : cours, formules et exercices pour progresser

La trigonométrie fait partie des notions clés abordées en classe de 3ème. Elle permet de résoudre des problèmes liés aux triangles rectangles en utilisant des formules simples. Que tu sois en pleine révision pour un contrôle ou en préparation du Brevet, cette page t’aide à comprendre l’essentiel grâce à des explications claires, des exemples concrets et des exercices corrigés.  

Les bases à connaître pour réussir en trigonométrie en 3ème

Le triangle rectangle et ses propriétés

Avant de se lancer dans la trigonométrie, il faut bien comprendre ce qu’est un triangle rectangle. C’est un triangle qui possède un angle droit, c’est-à-dire un angle de 90°. C’est uniquement dans ce type de triangle que les formules de trigonométrie vues en 3ème sont valables.

Quelques propriétés essentielles à retenir :

• L’angle droit est toujours opposé au plus grand côté, appelé hypoténuse
• Les deux autres côtés sont appelés côtés de l’angle droit
• La somme des trois angles d’un triangle est toujours égale à 180°

Connaître ces points permet d’identifier rapidement les éléments nécessaires à un calcul trigonométrique.

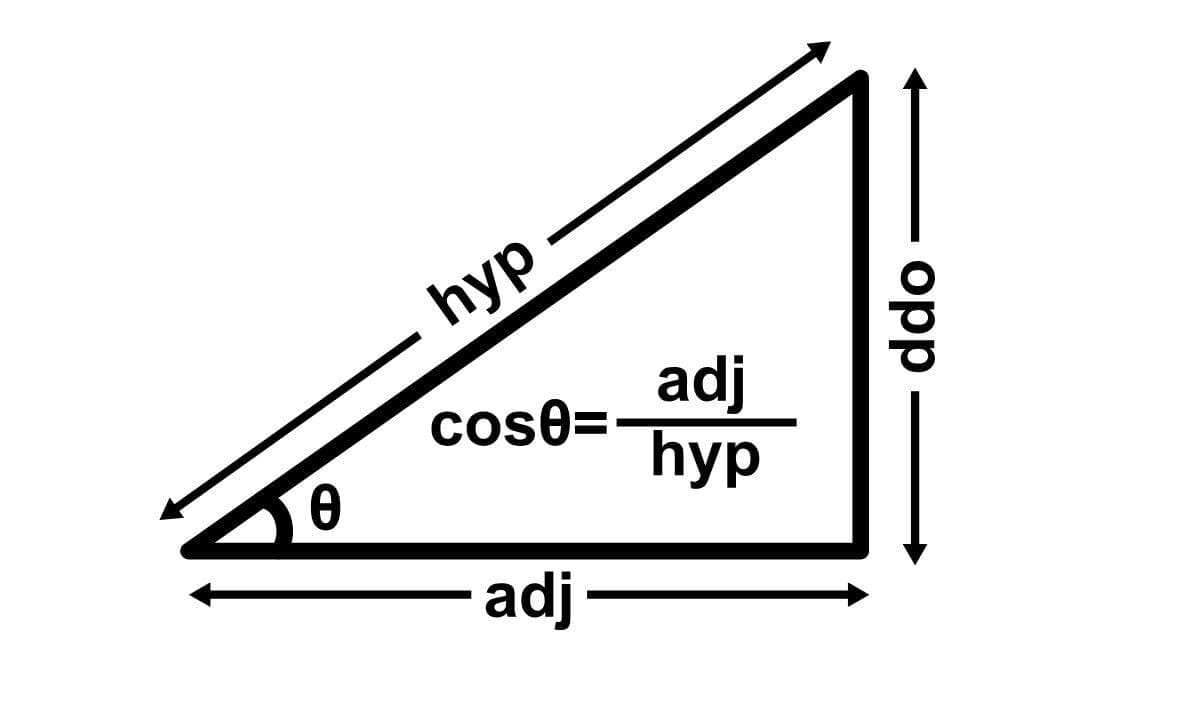
Le vocabulaire à maîtriser (hypoténuse, angle droit…)

Pour bien utiliser les formules de trigonométrie, il est important de bien nommer les éléments du triangle. Voici les mots clés à connaître :

• Hypoténuse : le plus grand côté du triangle, toujours en face de l’angle droit
• Côté adjacent : le côté qui forme l’angle étudié avec l’hypoténuse
• Côté opposé : le côté qui est en face de l’angle étudié
• Angle aigu : un angle inférieur à 90°, utilisé pour appliquer les formules

En maîtrisant ce vocabulaire, tu pourras repérer les bons éléments dans un exercice et choisir la bonne formule à utiliser.

Formules de trigonométrie à retenir en 3ème

Cosinus, sinus et tangente expliqués simplement

En 3ème, tu apprends trois formules de trigonométrie à utiliser dans un triangle rectangle. Elles permettent de relier un angle à deux côtés du triangle :

• cosinus d’un angle = côté adjacent ÷ hypothénuse
• sinus d’un angle = côté opposé ÷ hypothénuse
• tangente d’un angle = côté opposé ÷ côté adjacent

Ces rapports sont très utiles pour calculer un angle ou une longueur lorsqu'on connaît deux éléments d’un triangle rectangle.

Comment choisir la bonne formule selon l’exercice

Le choix de la formule dépend des informations données dans l’exercice. Voici une méthode simple pour t’orienter :

Tu connais l’hypoténuse et un côté adjacent → utilise le cosinus
Tu connais l’hypoténuse et un côté opposé → utilise le sinus
Tu connais les deux côtés de l’angle droit (opposé et adjacent) → utilise la tangente
Avant de te lancer dans les calculs, repère toujours l’angle de référence et identifie les côtés par rapport à lui.

Astuce pour s’en souvenir facilement

Un moyen simple de retenir ces formules est d’utiliser une phrase mémo-technique :

"CAH SOH TOA" :

Cosinus = Adjacent / Hypoténuse
Sinus = Opposé / Hypoténuse
Tangente = Opposé / Adjacent

Cette phrase t’aide à ne pas te tromper dans les rapports et à aller plus vite lors des contrôles ou examens.

Méthodologie pour résoudre un triangle

Étapes à suivre pour appliquer une formule

Quand tu dois résoudre un triangle rectangle à l’aide de la trigonométrie, voici les étapes à suivre :

1. Identifier l’angle de référence : repère bien l’angle dont il est question dans l’énoncé
2. Nommer les côtés par rapport à cet angle : opposé, adjacent, ou hypothénuse
3. Choisir la bonne formule (cosinus, sinus ou tangente) selon les côtés connus
4. Remplacer les longueurs ou les valeurs dans la formule
5. Résoudre l’équation et penser à utiliser la calculatrice si besoin
6. Vérifier que le résultat est cohérent avec la figure ou l’énoncé

En suivant cette méthode, tu limites les erreurs et gagnes en efficacité.

Exemple d’exercice corrigé pas à pas

Énoncé : Dans un triangle rectangle, on connaît un angle aigu de 35° et la longueur de l’hypoténuse (10 cm). On cherche la longueur du côté adjacent à cet angle.

Étape 1 : On identifie l’angle (35°) et on note que l’on connaît l’hypoténuse et que l’on cherche le côté adjacent.

Étape 2 : La formule adaptée est le cosinus :
cos(35°) = adjacent / hypothénuse

Étape 3 : On remplace dans la formule :
cos(35°) = x / 10

Étape 4 : On résout :
x = 10 × cos(35°)
x ≈ 10 × 0,819 = 8,19 cm

Conclusion : La longueur du côté adjacent est d’environ 8,19 cm.

Ce type de raisonnement est à connaître pour réussir les exercices en contrôle ou au Brevet.

Télécharge dès maintenant notre application