Bac 2025 : les sujets corrigés de spécialité Physique-Chimie

Si tu es en Terminale avec la spécialité Physique-Chimie, dès la fin de l’épreuve du 17 juin, tu pourras retrouver les sujets officiels tombés au Bac 2025, ainsi que leurs corrigés complets rédigés par des enseignants de la discipline sur cette page. En attendant, on t’aide à aborder l’épreuve dans les meilleures conditions : focus sur les chapitres incontournables, les types d’exercices les plus fréquents et des conseils concrets pour t'entraîner efficacement.

 Introduction 

Cette page sera actualisée dès la publication officielle des sujets de Physique-Chimie le lundi 17 juin 2025.

Tu pourras y retrouver :

• Les énoncés du jour 1 (17 juin) et du jour 2 (18 juin, selon les académies)
• Les corrigés détaillés, rédigés par nos professeurs partenaires
• Des explications par étape, illustrées et pédagogiques
• Des conseils pour corriger tes erreurs et progresser

 
Les sujets et corrigés de spécialité Physique-Chimie du Bac 2025

Télécharger le sujet de l’épreuve de Physique-Chimie (jour 1)

 
Le corrigé de l’épreuve de Physique-Chimie (jour 1)

Voici une proposition de corrigé.

EXERCICE 1
Un emballage intelligent au rayon poissonnerie (9 points)

1. Synthèse du bleu de bromophénol

Q1. Etape 1 : transformation des réactifs  

Etape 2 : Séparation

Etape 3 : Analyse du produit brut  

Etape 4 : Analyse du produit brut 

Q2. On sait que le rouge de phénol a été introduit dans l'erlenmeyer.  

Or, le chromatogramme obtenu montre que le produit synthétisé brut à l’état final ne présente pas la tâche correspondant au rouge de phénol. Donc le rouge de phénol a disparu. donc une transformation chimique a eu lieu.  

Le produit synthétisé présente au moins deux tâches donc il n'est pas pur.

Q3. On voit sur le spectre que le BBP de référence absorbe au maximum à une longueur d'onde de 590nm tout comme le produit synthétisé donc il y a du BBP dans le produit brut.

Q4. On peut utiliser un banc Kofler qui est un dispositif utilisé pour identifier des solides, grâce à leur température de fusion.

2. Identification du produit synthétisé par une mesure de $pK_A$

Q5. $$K_A=\frac{[BH^-][H_3O^+]}{[BH_2]c^o}$$

Q6. En utilisant Q5, on a :

$$-\log\left(K_A\right)=-\log\left(\frac{[BH^-][H_3O^+]}{[BH_2]c^o}\right)$$

Donc en utilisant les propriétés de log et le fait que $c^o=1$mol/L, on a :

$$pK_A=-\log\left(\frac{[BH^-]}{[BH_2]}\right)+pH$$

Donc 

$$pH= pK_A+\log\left(\frac{[BH^-]}{[BH_2]}\right)$$

Q7. À l'équivalence les réactifs sont introduits dans les proportions stoechiométriques.

Q8. On trouve $V_{éq}=14.7$mL en utilisant la technique de la dérivée.

Q9. À la demi-équivalence, la moitié de $BH_2$ a réagi et s'est transformée en $BH^-$. Comme les coefficients stoechiométriques de la réactions sont égaux à 1, il reste autant de $BH_2$ que de $BH^-$ ne s'est formé, d'où :

$$[BH^-]=[BH_2]$$

Q10. On réutilise la formule démontrée en Q6 :

$$pH= pK_A+\log\left(\frac{[BH^-]}{[BH_2]}\right)$$

De plus, d'après Q9, à la demi-équivalence, on a $[BH^-]=[BH_2]$, donc :

$$pH= pK_A+\log 1$$

Donc $pH= pK_A$ à la demi-équivalence.

On trouve donc $pK_A=3.9$ en se plaçcant à $\frac{V_{éq}}{2}$ la figure 1.

Q11. On calcule le quotient :

$$\frac{\vert 3.9-4.1 \vert}{0.3}=0.67$$

Le z-score  est  inférieur  à  2  donc  la  valeur  obtenue en Q10 et  la  valeur  tabulée  sont  en accord.

3. Étude de la couleur de la pastille dans l'emballage intelligent 

Q12. D'après la figure 2, $\lambda_{max}=430$nm ce qui correspond à une couleur absorbée violette. Donc l'espèce apparait de la couleur complémentaire, à savoir : jaune car diamétralement   opposée   sur le cercle chromatique.

Q13. Pour calculer la concentration de la solution commerciale, on peut démontrer que :

$$c_{mère}=\frac{t_md\rho_{eau}}{M}$$

Donc l'application numérique donne :

$$c_{mère}=\frac{0.37 \times 1.18 \times 1.0 \times 10^3}{36.5}=12mol/L$$

Or on veut préparer une solution de concentration :

$$c_{fille}=10^{-pH}=1.0\times 10^{-2}mol/L$$

On sait que pour une dilution :

$$c_{mère}V_{mère}=c_{fille}V_{fille}$$

Donc

$$V_{mère}=\frac{c_{fille}V_{fille}}{c_{mère}}$$

Donc 

$$V_{mère}=\frac{1.0\times 10^{-2} \times 200.0}{12}=17mL$$

Il n'y a pas de fiole jaugée de 17mL qui soit proposée donc cette dilution n'est pas possible.

Q14. Molécule B

Q15. 

$$BH_2+R_3N \rightarrow BH^- + R_3NH^+$$

4. Cinétique d'ordre 1 de la décoloration du BBP en présence d'ion hydroxyde

Q16. $BH^-$ présente à la fois un caractère acide et basique.

Q17. D'après la figure 4, $t_{1/2}= 775s$.

EXERCICE 2
Datation d'une roche (6 points)

1. Le rubidium 87, un isotope radioactif adapté pour dater une roche

Q1. Des noyaux isotopes ont même nombre de protons mais nombres de neutrons différents.

Q2. 

$$^{87} _{37}Rb \rightarrow ^{87} _{38}Sr + ^{0} _{-1}e$$

Q3. Désintégration $\beta ^-$.

Q4. Temps nécessaire pour que la moitié des atomes d'un échantillon se désintègrent naturellement.

Q5. D'après l'énoncé :

$$2^{38}<\frac{5.8\times 10^{20}}{2\times 10^{9}}<2^{39}$$

Donc

$$\frac{5.8\times 10^{20}}{2^{39}}<2\times 10^{9}$$

Donc au bout de 39 demi-vies, on est en-dessous du seuil minimum détectable. 

Donc le nombre maximal de demi-vies après lequel il reste suffisamment de rubidium 87 dans l’échantillon pour qu’on puisse le détecter est de : 38 demi-vies.

Q6. On a vu en Q5 qu'on peut dater  des échantillons vieux de 38 demi-vies, c'est-à-dire $38 \times 49.2 \times 10^9=1.9 \times 10^{12}$ années.  

Or, la roche du site de Meymac est âgée de plusieurs centaines de millions d'années. Sachant que cent millions d'année correspond à $1\times 10^8$ ans, on est bien en-dessous du seuil maximal.

2. Décroissance radioactive du rubidium 87 dans une roche

Q7. On calcule la dérivée de $N_{Rb}(t)$ :

$$\frac{dN_{Rb}(t)}{dt}=\frac{d \left(N_{Rb}(0).e^{-\lambda \times t}\right)}{dt}=-\lambda.N_{Rb}(0).e^{-\lambda \times t}=-\lambda.N_{Rb}(t)$$

Donc $N_{Rb}(t)$ est bien solution de l'équation différentielle.

Q8. 

$$N_{min}=N_{Rb}(0).e^{-\lambda . t_f}$$

D'où

$$\ln \frac{N_{min}}{N_{Rb}(0)}=-\lambda . t_f$$

On isole $t_f$

$$t_f=\frac{-1}{\lambda}\ln \frac{N_{min}}{N_{Rb}(0)}$$

Q9.

L'application numérique donne : 

$$t_f=1.9 \times 10^{12} ans$$

Commentaire : On trouve exactement le même résultat ce qui n'est pas étonnant car nous avons simplement calculé de deux manières différentes la même grandeur.

3. Datation d'une roche du site de Meymac au strontium 87

Q10. 

$$N_{Sr\:formé}(t)=N_{Rb}(0)-N_{Rb}(t)$$

Q11. On sait que :

$$N_{Rb}(t)=N_{Rb}(0).e^{-\lambda \times t}$$

Donc :

$$N_{Rb}(0)=N_{Rb}(t).e^{\lambda \times t}$$

Donc en utilisant Q10 :

$$N_{Sr\:formé}(t)=N_{Rb}(t).e^{\lambda \times t}-N_{Rb}(t)$$

On factorise par $N_{Rb}(t)$ :

$$N_{Sr\:formé}(t)=N_{Rb}(t)\left(e^{\lambda \times t}-1 \right)$$

Q12. D'après l'équation 3 et la figure 1, on a :

$$e^{\lambda .t}-1=0.0042$$

On isole $t$ :

$$t=\frac{ln(1+0.0042)}{\lambda}$$

L'application numérique donne $t=3.0 \times 10^8$ ans, soit environ 300 millions d'années ce qui est cohérent avec les informations données dans l'introduction.

EXERCICE 3
Viscosimètre à chute de bille (5 points)

Q1. D'après la formule de la force de frottement donnée dans l'énoncé, on sait que la viscosité est homogène à une force sur une longueur fois une vitesse, c'est-à-dire $\frac{N}{m.m.s^{-1}}$ ce qui revient à $N.m^{-2}s$.

Q2. D'après la formule de la force de frottement donnée dans l'énoncé, la norme de la force est proportionnelle à la vitesse donc plus la vitesse est grande, plus la force de frottement est grande.

Q3. D'après la première loi de Newton, comme la bille est en mouvement rectiligne uniforme alors la somme des forces qui s'exercent sur elle se compensent. D'où le schéma en prenant soit de faire la taille du vecteur poids de même longueur que la somme des vecteurs des forces de frottement et poussée d'Archimède.

Q4. 

Système : {Bille}  

Référentiel terrestre supposé galiléen  

Bilan des forces : Poids, frottement, poussée d'Archimède  

Première loi de Newton projeté sur l'axe (Oz): 

$$mg-\alpha . \eta_C .v_{lim}-\rho _h . V_b.g = 0$$

En utilisant $m=\rho_b \times V_b$ et $V_b=4/3.\pi.r^3$, on trouve la formule demandée.

Q5. On trouve $\eta = 8.94 \times 10^{-2}N.m^{-2}.s$

Q6. Le calcul du z-score donne un résultat inférieur à 2 donc les deux valeurs sont en accord.

Q7. Seconde loi de Newton appliqué à la bille projeté sur l'axe (Oz): 

$$mg-\alpha . \eta_C .v-\rho _h . V_b.g = m.a$$

Donc

$$a=\frac{mg-\alpha . \eta_C .v-\rho _h . V_b.g}{m} $$

D'où la relation demandée après simplification.

Q8. Pour trouver l'équation demandée, on utilise le résultat de Q7 en remplaçant $a=\frac{dv}{dt}$ 

et $m=\rho_b \times V_b = \rho_b\times 4/3.\pi.r^3$

Q9. On trouve $\tau = 2.4 \times 10^{-3}s$.

La vitesse limite est atteinte au bout de $5\tau$, soit $1.2 \times 10^{-2}s$.

Sachant que la vitesse maximale de la bille est $v_{lim}$, on peut en déduire que la bille mettra au minimum $\Delta t = \dfrac{0.15}{5.37 \times 10^{-3}}=28$s pour descendre le tube. On peut donc considérer que la vitesse de la bille est pratiquement égale à sa valeur limite durant tout le mouvement.

 
Télécharger le sujet de l’épreuve de Physique-Chimie (jour 2)

 
Le corrigé de l’épreuve de Physique-Chimie (jour 2)

Voici une proposition de corrigé.

Exercice 1
Mesure de l'épaisseur d'un film alimentaire (11 points)

1. Mesure de l'épaisseur d'un film alimentaire par capacimétrie

Q1. En appliquant la loi des mailles, on a :

$$E = u_R(t) + u_C(t)$$

Or, la tension aux bornes de la résistance est d'après la loi d'Ohm :

$$u_R = R \cdot i$$

Et on sait que pour un condensateur :

$$i = C \cdot \frac{du_C}{dt}$$

Donc :

$$u_R = R \cdot C \cdot \frac{du_C}{dt}$$

Donc en remplaçant dans la loi des mailles donnée plus haut, on obtient :

$$E = R \cdot C \cdot \frac{du_C}{dt} + u_C$$

On obtient alors l’équation différentielle du circuit RC :

$$RC \cdot \frac{du_C}{dt} + u_C = E$$

On pose $\tau=RC$ et on divise les deux membres par $\tau$ ce qui donne bien :

$$\frac{du_C}{dt} + \frac{1}{\tau}{u_C} = \frac{E}{\tau}$$

Q2. quand $t$ tend vers l'infini, le condensateur est chargé donc $\lim _{\infty}cu_C(t)=E$. Donc :

$$\lim _{\infty} A\left( 1-e^{-\frac{t}{\tau}} \right)=E$$

Donc : 

$$A=E$$

Q3. On a :

$$u_C(\tau)= E\left( 1-e^{-\frac{\tau}{\tau}} \right)$$

Donc

$$u_C(\tau)= E\left( 1-e^{-1} \right)$$

Remarque : Un calcul approché donne $u_C(\tau)= 0,63E$

Q4. On trouve graphiquement :

$$\tau = 63 \mu s$$

Q5. On sait que $\tau=RC$ donc :

$$C=\frac{\tau}{R}$$

L'application numérique donne :

$$C=6,3 \times 10^{-9} F$$

Q6. En utilisant la formule présente dans les données, on a :

$$e_{film}=\frac{\epsilon_0 \cdot \epsilon_r \cdot S}{C}$$

L'application numérique donne :

$$e_{film}=1,7 \times 10^{-5}m$$

Q7. On calcule le z-score et on trouve 9,5 ce qui est supérieur à 2 donc le résultat obtenu à la question Q6 n'est pas en accord avec la valeur de l’épaisseur de référence du film indiquée dans les données.

Q8. Premier cas limite : il n'y a pas du tout d'air et alors $e_{air}=0$ et on retrouve la formule présente dans les données.  

Deuxième cas limite : il n'y a pas du tout de film mais que de l'air et alors $e_{film}=0$ et on retrouve la formule présente dans les données.

Q9. En utilisant la formule de $C'$ donnée dans l'énoncé, on trouve :

$$\frac{e_{air}}{\epsilon_{r,air}}+\frac{e_{film}}{\epsilon_{r,film}}=\frac{\epsilon_O \cdot S}{C'}$$

Donc

$$\frac{e_{air}}{\epsilon_{r,air}}=\frac{\epsilon_O \cdot S}{C'}-\frac{e_{film}}{\epsilon_{r,film}}$$

On isole $e_{air}$ et on obtient :

$$e_{air}=\epsilon_{r,air} \left( \frac{\epsilon_O \cdot S}{C'}-\frac{e_{film}}{\epsilon_{r,fim}}\right)$$

L'application numérique donne :

$$e_{air}=4,2 \times 10^{-6}m$$

Commentaire : Le film aurait donc en réalité une épaisseur $e_{air}+e_{film}=4,2 \times 10^{-6}+7,6 \times 10^{-6}=1,2 \times 10^{-5}m$ ce qui est plus proche de la valeur trouvée en Q6.

2. Mesure de l'épaisseur du film alimentaire par pesée

Q10. On sait que :

$$m_{film}=\rho \cdot V=\rho \cdot l \cdot L \cdot e_{film}$$

Donc

$$e_{film}=\frac{m_{film}}{\rho \cdot l \cdot L}$$

L'application numérique donne :

$$e_{film}=6,5 \times 10^{-6}m$$

3. Mesure de l'épaisseur du film alimentaire par interférométrie

Q11. Dans le cas d'interférences constructives :

$$\delta = k \lambda$$

avec $k$ un entier relatif.

Q12. Si $\frac{\beta \times e_{film}}{\lambda}$ est un entier alors $p=\frac{\beta \times e_{film}}{\lambda}+\frac{1}{2}$ est un demi entier. Donc, $p=\frac{\delta}{\lambda}$ est un demi entier, donc on observe dans ce cas un phénomène d'interférences destructives.

Q13. Ils ont pour origine le phénomène d'interférences constructives.

Q14. La relation (1) peut se réecrire :

$$p=\beta \times e_{film} \times \frac{1}{\lambda}+\frac{1}{2}$$

On voit ainsi que $p$ en fonction de $1/\lambda$ est une fonction affine ce qui est cohérent avec la figure 7.

Q15. En utilisant le coefficient directeur, on a $22443\times 10^{-9}=\beta \times e_{film}$. On trouve alors après calcul :

$$e_{film}=\frac{22443\times 10^{-9}}{3,02}=7,4 \times 10^{-6}m$$

Commentaire : Résultat cohérent avec la valeur de $7,6 \times 10^{-6}m$ donnée dans l'énoncé.  

(On ne peut pas calculer le z-score car avec cette méthode $u(e_{film})$ n'est pas donné).

Exercice 2
Eau de Quinton (4 points)

1. Préparation de l'eau de Quinton isotonique

Q1. On souhaite réaliser une dilution d'un facteur $F=5$ donc le volume de solution mère à prélever est $\frac{100}{5}=20,00mL$.

Protocole de la dilution :  

1. Verser la solution mère, solution commerciale d'eau de Quinton, dans un bécher de 100mL.  

2. À l’aide d’une pipette jaugée de  20mL, prélever 20mL de la solution mère contenue dans ce bécher.  

3. Verser ce prélèvement dans une fiole jaugée de 100 mL.  

4. Ajouter de l’eau distillée au 3/4.  

5. Boucher, agiter.  

6. Ajouter de l'eau distillée jusqu’au trait de jauge. 

7. Boucher, agiter.  

Q2. Après dilution, on aura :

$$c_{fille}=\frac{c_{mère}}{F}$$

On trouve grâce aux données : 

$$c_{mère}=\frac{19,4}{35,5}=0,546mol/L$$

Donc :

$$c_{fille}=\frac{\frac{19,4}{35,5}}{5}=0,109mol/L$$

Cela correspond à 109mmol/L. La solution est donc bien isotonique.

2. Analyse d'une eau de Quinton hypertonique

Q3. La réaction du titrage est :

$$Cl^-_{(aq)}+Ag^+_{(aq)} \rightarrow AgCl_{(s)}$$

Q4.   

A correspond à $Cl^-$ dont la concentration diminue avant l'équivalence puis devient nulle après puisqu'il est le réactif titré.    

B correspond à $Ag^+$ dont la concentration est nulle avant l'équivalence puis augmente après puisqu'il est le réactif titrant.    

C correspond à $NO_3^-$ dont la concentration ne fait qu'augmenter car c'est un ion spectateur présent dans la solution titrante.

D correspond à $Na^+$ dont la concentration reste constante car c'est un ion spectateur présent dans la solution titrée.  

Q5. D'après 

$$V\_E=C\_1 * V\_1 / C_2$$

Q6. Avant l'équivalence, $[Cl^-]$ diminue et $[NO_3^-]$ augmente, les autres ions ont des concentrations constantes. Or d'après les données, la conductivité molaire ionique de $Cl^-$ est plus grande que celle de $NO_3^-$ donc la conductivité de la solution diminue. 

Après l'équivalence, $[NO_3^-]$ et $[Ag^+]$ augmentent, les autres ions ont des concentrations constantes, donc la conductivité de la solution augmente.

Q7. D'après la figure A1,$V_{éq}=18,5mL$ donc la concentration titrée est :

$$C_1=\frac{C_2\cdot V_{éq}}{V_1}$$

L'application numérique donne :

$$C_1=\frac{3,00 \times 10^{-1}\cdot 18,5}{10,0}=5,55 \times 10^{-1} mol/L$$

Comme avant le titrage, il y avait eu une dilution de facteur $F=210/10=21$ alors la concentration recherchée est :

$$C_{Quinton}=21 \times C_1$$

L'application numérique donne :

$$C_{Quinton}=12 mol/L$$

Q8. On calcule la concentration massique :

$$Cm_{Quinton}=C_{Quinton} \times M(Cl)$$

Cela donne :

$$Cm_{Quinton}=19,7g/L$$

en gardant 3C.S.  

Donc : 

$$Cm_{Quinton}=2,0 \times 10^{1}g/L$$

en gardant 2C.S.

En réalisant le calcul du z-score, on trouve un z-score de 3 ce qui est supérieur à 2 donc la concentration trouvée n'est pas en accord avec la concentration en ions chlorure de l’eau de mer bretonne.

Exercice 3
Un parfum de rose (5 points)

1. Étude préliminaire

Q1. C'est le groupe hydroxyle.  

Famille du géraniol : alcool et alcènes  

Famille de l’éthanoate de géranyle : ester et alcène

Q2. On voit sur le spectre de la figure 1 : 

•  une bande forte et fine vers $1740 cm^{-1}$ caractéristique de la liaison C=O présente dans les esters.   
• une absence de bande forte entre $3200$ et $3700 cm^{-1}$, bande caractéristique des alcools.

On en conclut qu'il s'agit du spectre de l’éthanoate de géranyle.

2. Transformation du géraniol en éthanoate de géranyle

Q3. Un catalyseur est une substance qui augmente la vitesse d'une réaction chimique sans apparaître dans le bilan de la réaction. 

L'estérification présentée est catalysée par $H^+$ car on voit qu'il est consommé au départ puis régénéré à la fin.

Q4. 

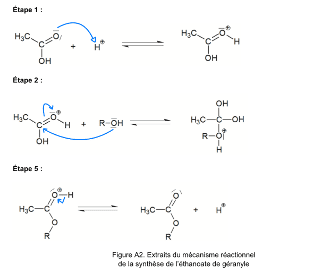
Q5. A est $H_2O$.

L’équation de la réaction d'estérification est :  

$CH_3COOH_{(l)} + R{-}OH_{(l)} \leftrightarrow H_2O_{(l)} + CH_3COO{-}R_{(l)}$

Q6. On sait que la température est un facteur cinétique donc l'intérêt de chauffer est d'augmenter la vitesse de la réaction.

Q7. La phase aqueuse est de densité 1,0. La densité du géraniol et de l’éthanoate de géranyle sont respectivement de 0,89 et 0,92 donc dans l'ampoule à décanter :  

• La phase organique contenant le géraniol et l’éthanoate de géranyle est au-dessus
• La phase aqueuse est en dessous et contient de l'eau et de l'acide

Q8. 

On a $n_A=C_A \cdot V_A = 5,0 \times 10^{-2} mol$.

On a $n_G=\dfrac{m_G}{M_G} = 5,0 \times 10^{-2} mol$.

On a donc :

$$\dfrac{n_A}{1}=\dfrac{n_G}{1}$$

Donc l’acide éthanoïque et le géraniol sont introduits dans les proportions stœchiométriques.

Q9. L'équation du titrage est :

$$CH_3CO_2(aq)+HO^-(aq) \rightarrow CH_3COO^-(aq)+H_2O(l)$$

D'après la figure 2 et en utilisant la méthode des tangentes on trouve $V_{éq}=33mL$.

À l'équivalence, on a la relation :

$$\dfrac{n_{CH_3CO_2H}}{1}=\dfrac{n_{HO^-}}{1}$$

Donc

$$\dfrac{n_{CH_3CO_2H}}{1}=c_B \times V_{éq}=3,3 \times 10^{-2} mol$$

Q10. Le rendement est donné par :

$$\eta = \frac{n(ester)_{exp}}{n(ester)_{théorique}}$$

On a :

$$n(ester)_{exp}=5,0 \times 10^{-2}-3,3 \times 10^{-2}=1,7 \times 10^{-2} mol$$

On a :

$$n(ester)_{théorique}=5,0 \times 10^{-2}mol$$

On peut donc caluler le rendement et on trouve :

$$\eta = 34%$$

3. Utilisation du géraniol en parfumerie

Q11.

•  Étape 1 : On cherche la masse maximale de géraniol à laquelle une personne de 65 kg peut être exposée :
  $$65 \times 17{,}75 = 1,15 \times 10^3 ~\text{mg} = 1{,}15g$$

• Étape 2 : On cherche la masse de parfum dans une pulvérisation :
  $$m_{\text{parfum}} = \rho_{\text{parfum}} \cdot V_{\text{parfum}} = 0{,}84 \times 0{,}15 = 0{,}126g$$
  
  
• Étape 3 : On cherche la masse de géraniol contenue dans une pulvérisation sachant que le parfum contient 0,001 % en masse de géraniol :
  $$m_{\text{géraniol}} = 0{,}126 \times \dfrac{0{,}001}{100} = 1{,}26 \times 10^{-6}~\text{g}$$
  
  
• Étape 4 : On cherche le nombre de pulvérisations permettant d'atteindre la dose limite :
  On sait que 1 pulvérisation correspond à $1{,}26 \times 10^{-6}$ g de géraniol.   
  Donc le nombre $n$ de pulvérisations correspondant à $1{,}15$ g est :
  $$n = \dfrac{1,15}{1{,}26 \times 10^{-6}} = 9,1 \times 10^{5}$$
• Étape 5 : Conclusion
  Il faudrait donc plus de $9,1 \times 10^{5}$ pulvérisations pour que la personne atteigne la dose limite ce qui est énorme. Il n'y a donc pas de risque de mise en danger.

 
Bien se préparer à l’épreuve de Physique-Chimie

Structure de l’épreuve

• Durée : 4 heures
• Format : 3 exercices indépendants, tous obligatoires
• Notions abordées : formulation chimique, transformations acide-base, mécanique, ondes, électrocinétique, spectres IR/UV, dosages, réactions d’oxydoréduction…
• Les sujets mélangent habilement modélisation, calcul, interprétation de résultats expérimentaux et analyse critique.

 
Les points clés à maîtriser

Pour maximiser tes chances, concentre-toi, sans faire d'impasse sur le programme, sur les thèmes les plus souvent abordés :

• Cinétique chimique et suivi temporel d’un système
• Interactions fondamentales et lois de Newton
• Chimie organique et stœchiométrie
• Électricité, lois de l’électrocinétique et circuits RC
• Spectroscopie IR, RMN, UV-visible
• Ondes mécaniques et lumineuses

Voir les contenus de Terminale Spécialité Physique-Chimie sur Nomad Education

 
Réviser efficacement avec Nomad Education

Nomad t’aide à transformer ta révision en entraînement ciblé :

• Mini-fiches synthétiques pour chaque notion du programme
• Quiz progressifs avec explications détaillées
• Annales corrigées pour se mettre en conditions
• Exercices corrigés pas à pas, y compris les raisonnements attendus
• Paires parfaites, flashcards et astuces pour mémoriser les formules

Avec Nomad, tu passes de la révision passive à une approche active, logique et structurée.

Découvrir les contenus de Physique-Chimie

 
FAQ Bac Physique-Chimie 2025

Quand a lieu l’épreuve de Physique-Chimie au Bac ?

L’épreuve écrite a lieu le lundi 17 juin 2025 et le mardi 18 juin. 

Où retrouver les sujets et corrigés ?

Directement sur cette page, dès leur publication. Les corrigés seront mis en ligne dans l’après-midi, exercice par exercice.

Est-ce qu’il y a des calculatrices autorisées ?

Oui, une calculatrice avec mode examen est autorisée. Pense à la tester à l’avance et à bien la paramétrer.

Comment optimiser ses révisions à quelques jours de l’épreuve ?

Fais une liste des chapitres que tu maîtrises le moins. Travaille-les en priorité avec des fiches condensées, des annales ciblées et des exercices corrigés. Et n’oublie pas de t’entraîner en condition réelle.

Est-ce que les barèmes sont stricts ?

La Physique-Chimie reste une épreuve technique : la clarté des démarches, les unités, la logique et la précision du vocabulaire scientifique sont pris en compte dans la notation.

 
Ce qu’il faut retenir

Cette page sera ton point d’appui pour l’épreuve de spécialité Physique-Chimie. D’ici le 17 juin, continue à t’entraîner régulièrement. Le jour J, applique la méthode, garde ton sang-froid, et viens ici pour retrouver les sujets et corrigés officiels. Toute l’équipe Nomad Education est à tes côtés pour t’aider à viser la mention.